Timing tools

[In work! You might use it as a reference in the meantime, but some things are not yet covered. Also let me know if things are not clear! -- VG]

Foucalc

The basic tool for X-ray timing analysis with the Remeis scripts is foucalc , which calculates power-, cross power-, coherence- and timelag-spectra . It requires equally spaced, gapless lightcurves as well as the length of the lightcurve segment on which the Fourier transformation is to be performed, given in number of bins. Note that because the underlying algorithm is FFT, the segment length should be a power of two to increase the performance.

When only one lightcurve is given, foucalc calculates the power density and related quantities only. When more than one lightcurve is given, the cross power-, coherence- and timelag-spectra are calculated for all pairs of lightcurves. The lightcurves have to be in the format:

lc = struct { time=[t_1, t_2, ...], rate1=[r1_1, r1_2, ...], rate2=..., rate3= };

The time has to be given in seconds (so be cautious when using fits_read_lc, which usually returns the time in MJD).

If you use RXTE/PCA lightcurves, don't forget to set the numinst keyword, which defines the number of instruments (=PCUs) on, since otherwise your noise correction will be wrong. If you are not using RXTE/PCA set the deadtime keyword to whatever is appropriate for the instrument you are using (e.g. 0).

Given a single PSD value before any further calculations, its uncertainty will be of the same order of magnitude as the PSD itself. Averaging therefore crucial. This is build in into foucalc: given a lightcurve of say 1288192 bins and a segment length of 16384, foucalc will calculate a PSDs on every segment and average every value over all 1288192/15385 = 78 segments.

PSDs

Calculating the PSD

Given two PCA lightcurves,

50110-01-45-00_437_AND_good_14off_excl_0-10.lc

and

50110-01-45-00_437_AND_good_14off_excl_11-13.lc

(which have been checked for gaps and found to be gapless ) we want to calculate and bin the PSD, lags and coherence.

%% read in lightcurves
variable lc1 = fits_read_table("50110-01-45-00_438_AND_good_14off_excl_0-10.lc");
variable lc2 = fits_read_table("50110-01-45-00_438_AND_good_14off_excl_11-13.lc");

%%define variables to store average rate of lightcurve & rms
variable rms,avg;

%%calculate timing quantities
variable result = foucalc(struct{time=lc1.time,rate1=lc1.rate,rate2=lc2.rate},16384;
                          numinst=3,RMS=&rms,avgrate=&avg,verbose);

This produces the following output - thank to the verbose keyword:

light curves: 2516 s with 1288192 bins of 0.00195312 s  (0 s gaps)
  segmentation: 78 segments of 16384 bins
=> frequencies: 0.03125-256 Hz.
Power spectra will be calculated in Miyamoto-normalization.
Calculating power spectrum for rate1.  RMS(0.03125-256 Hz) = 27.1%
Calculating power spectrum for rate2.  RMS(0.03125-256 Hz) = 25.7%
Calculating cross power spectrum (=> coherence and timelags) for rate1 and rate2.

This is right now the only place at which foucalc will complain if the lightcurve contains gap. It will calculate the quantities even if the lightcurve contains gaps - only you can't trust your results. Therefore: use verbose, check that you've done everything right, at least while building up your scripts.

Plot the PSD for the first lightcurve with:

xlog;ylog;plot_with_err(result.freq,result.signormpsd1,result.errnormpsd1);

Rebinning the PSD

The uncertainties on the individual PSDs values are still large, especially at high frequencies. To further improve the SNR, the PSD is rebinned to a new frequency grid and the final PSDs is then the average over the individual PSDs at the frequencies corresponding to the frequencies included into the new frequency bin. Mostly, a logarithmic rebinning with df/f = const. is used, a typical value would be df/f = 0.15 .

Quantities calculated with foucalc are rebinned with the rebin_fouquan tool - the quantity and it's error have to be rebinned in two individual steps:

variable reb_psd = rebin_fouquan(result.freq,result.signormpsd1,
                                 result.numavgall;logfreq=0.15);
variable reb_err = rebin_fouquan(result.freq,result.errnormpsd1,
                                 result.numavgall;logfreq=0.15);

reb_err does not yet contain the real errors of the psds, but needs to be weighted with the square root of the number of values the averaging was performed over. The final PSD is therefore:

variable psd1 = struct{freq_lo = reb_psd.freq_lo,freq_hi=reb_psd.freq_hi,
  value = reb_psd.value, error= reb_err.value/sqrt(reb_err.n)};

Once again plot you PSD - either as PSD vs. frequency or PSD x frequency vs. frequency:

%%PSD vs. frequency
xlog;ylog;plot_with_err((psd1.freq_lo+psd1.freq_hi)/2,psd1.value,psd1.error);

%%PSDxfreuency vs. frequency
xlog;ylog;plot_with_err((psd1.freq_lo+psd1.freq_hi)/2, psd1.value*(psd1.freq_lo+psd1.freq_hi)/2,
psd1.error*(psd1.freq_lo+psd1.freq_hi)/2);

Lag-energy spectrum for archival XMM-Newton data

The following is an example how to compute PSDs, a lag-frequency spectrum, and a lag-energy spectrum on archival XMM-Newton data of GX 339-4 (written by OK, please ask if something is unclear) .

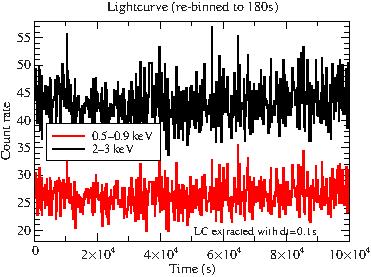
We start with extracting the lightcurve in two energy bands (500-900eV and 2000-3000eV) with

#!/bin/tcsh
source $SOFTDIR/sas_init.csh # initialize the SAS software
set xmmscripts=${XMMTOOLS} # make sure the proper xmmscripts are loaded
set obsid='0204730201'
set datadir=/userdata/data/koenig/GX339-4/XMM-2004-03-16/odf
set dt=0.1

${xmmscripts}/xmmprepare --datadir=$datadir --prepdir=$obsid --pn --noapplyflaregti --timing --notimelog # prepare the data

${xmmscripts}/xmmextract --prepdir=$obsid --pn --timing --full --energyband="500,900" --noflarescreen --defaultpattern --dt=$dt --clobber

Now we load the data and correct them for the telemetry drop-outs (encoded in the Good Time Intervals):

%% Load the lightcurve and GTI file
a=fits_read_table("full_sd_0.1s_0500-0900.lc");
b=fits_read_table("full_sd_0.1s_2000-3000.lc");
gtia=fits_read_table("full_sd_0.1s_0500-0900.lc[GTI0006]");
gtib=fits_read_table("full_sd_0.1s_2000-3000.lc[GTI0006]");

%% Get the start time such that LC starts at 0s
tstart=fits_read_key("full_sd_0.1s_0500-0900.lc[1]", "TSTART");

%% Subtract TSTART and do GTI correction
(filta,filtb)     = filter_gti(a.time, gtia), filter_gti(b.time,gtib);
(timea,timeb)     = a.time[filta]-tstart,b.time[filtb]-tstart;
(countsa,countsb) = a.counts[filta],b.counts[filtb];

If we plot the (re-binned) lightcurve, there is not much to see.

File:Gx399m4 xmm lc.pdf

But, we can do a Fourier analysis in order to reveal the variability and correlations of these lightcurves (and ignore the warnings of foucalc if verbose is set that there are gaps in the lightcurve).

%% Choose segment length
dimseg=8192; %% (bins), should be a power of 2 for FFT

%% Compute PSDs, CPD, and time lags with foucalc
r=foucalc( struct{time=timea, rate1=countsa/dt, rate2=countsb/dt}, dimseg ; normtype="Miyamoto");
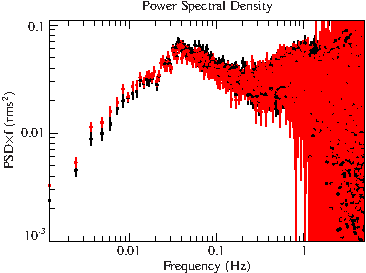
xlog;ylog;plot_with_err(r.freq,r.signormpsd1*r.freq,r.errnormpsd1*r.freq);

File:Gx399m4 xmm psd unbinned.pdf

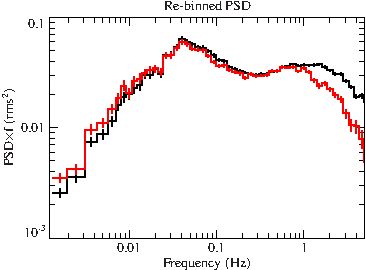
This really needs some re-binning to increase the S/N-ratio, which can be done with the rebin_fouquan routine.

%% Choose Delta f/f, the logarithmic frequency resolution
dff=0.15
reb_psd1 = rebin_fouquan(r.freq, r.signormpsd1, r.numavgall ; logfreq=dff);
reb_err1 = rebin_fouquan(r.freq, r.errnormpsd1, r.numavgall ; logfreq=dff);
reb_psd2 = rebin_fouquan(r.freq, r.signormpsd2, r.numavgall ; logfreq=dff);
reb_err2 = rebin_fouquan(r.freq, r.errnormpsd2, r.numavgall ; logfreq=dff);

%% Need to weight the PSD error with the square root of the number of values the averaging was performed over
psd1 = struct{
  freq_lo = reb_psd1.freq_lo,
  freq_hi = reb_psd1.freq_hi,
  value   = reb_psd1.value,
  error   = reb_err1.value/sqrt(reb_err1.n)
};
psd2 = struct{
  freq_lo = reb_psd2.freq_lo,
  freq_hi = reb_psd2.freq_hi,
  value   = reb_psd2.value,
  error   = reb_err2.value/sqrt(reb_err2.n)
};

plot_with_err((psd1.freq_lo+psd1.freq_hi)/2, psd1.value*(psd1.freq_lo+psd1.freq_hi)/2, psd1.error*(psd1.freq_lo+psd1.freq_hi)/2);

File:Gx339m4 xmm psd binned.pdf