3D orbit plots (xfig example)

The projection and handling of plotting in 3D is very similar to the examples Plotting in 3D (simple) and Plotting in 3D.

%-*- mode: fold; mode: slang -*-
require("isisscripts");

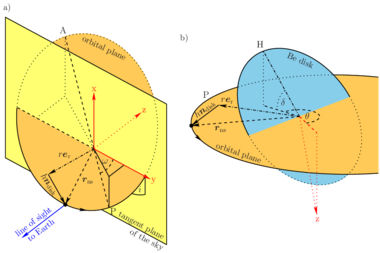
% we will produce two plots: one showing the orbital plane in the
% context of the tangent plane of the sky and, thus, defining the
% orbital elements. the second one defines the Be disk geometry
% with respect to the orbital plane only, i.e, *without* the
% tangent plane of the sky and the orbital elements.

% in the coordinate system used here, the tangent plane of the sky
% is defined as the xy-plane and the z-axis points away from Earth.
% that is with a camera inclination and roll angle of zero, we are
% looking directly onto the tangent plane of the sky. note that the
% x and y axis points north and east, respectively, i.e., the xy
% axis are flipped to ensure a right handed coordinate system.

xfig_add_latex_package("bm"); % for bold and italic fonts in mathmode
xfig_set_latex_preamble("\let\mathbfit\bm"R); % alias for MNRAS
xfig_set_font_style(NULL); % no bold face anywhere

%%% implement camera object %{{{

% set up the camera view port
private define _xfig_camera_setup(s, incl, zrot, roll) {
  s.camera_data.incl = incl;
  s.camera_data.zrot = zrot;
  s.camera_data.roll = roll;
  % update camera vectors
  s.camera_data.cx = vector_rotate(
    vector(1,0,0), vector(0,1,0), -s.camera_data.zrot*PI/180
  );
  s.camera_data.cy = vector_rotate(
    vector_rotate(vector(0,1,0), vector(1,0,0), s.camera_data.incl*PI/180),
    vector(0,1,0), -s.camera_data.zrot*PI/180
  );
  % optical axis of the camera
  variable camaxis = crossprod(s.camera_data.cx, s.camera_data.cy);
  % rotate around this vector
  s.camera_data.cx = vector_rotate(s.camera_data.cx, camaxis, s.camera_data.roll*PI/180);
  s.camera_data.cy = vector_rotate(s.camera_data.cy, camaxis, s.camera_data.roll*PI/180);
}

% add polygons to the plot
private define _xfig_camera_plot_polygon(s, v) {
  % add starting point [0,0,0]
  if (length(v.x) == 1 && not qualifier_exists("skiporigin")) {
    v = struct_copy(v);
    v.x = [0, v.x];
    v.y = [0, v.y];
    v.z = [0, v.z];
  }
  % add to list
  list_append(s.camera_data.polygons, v);
  list_append(s.camera_data.polygons_qualifiers, __qualifiers);
}

% add shaded region to the plot
private define _xfig_camera_shade_region(s, v) {
  % add to the same list as for polygons, but set a qualifier
  list_append(s.camera_data.polygons, v);
  list_append(s.camera_data.polygons_qualifiers, struct_combine(
    __qualifiers, struct { _camera_shade_region }
  ));
}

% add label to the plot
private define _xfig_camera_xyzlabel() {
  variable s, v, l, dx = 0, dy = 0;
  switch (_NARGS)
    { case 3: (s, v, l) = (); }
    { case 5: (s, v, l, dx, dy) = (); }
  list_append(s.camera_data.labels, v);
  list_append(s.camera_data.labels, l);
  list_append(s.camera_data.labels, [dx, dy]);
  list_append(s.camera_data.labels_qualifiers, __qualifiers);
}

% render polygons
private define _xfig_camera_render_polygons(s, pl) {
  % loop over polygons
  variable i;
  _for i (0, length(s.camera_data.polygons)-1, 1) {
    % shade region
    if (s.camera_data.polygons_qualifiers[i] != NULL &&
	struct_field_exists(s.camera_data.polygons_qualifiers[i], "_camera_shade_region")) {
      pl.shade_region(
        dotprod(s.camera_data.polygons[i], s.camera_data.cx),
        dotprod(s.camera_data.polygons[i], s.camera_data.cy);;
        s.camera_data.polygons_qualifiers[i]
      );
    }
    % plot line
    else {
      pl.plot(
        dotprod(s.camera_data.polygons[i], s.camera_data.cx),
        dotprod(s.camera_data.polygons[i], s.camera_data.cy);;
        s.camera_data.polygons_qualifiers[i]
      );
    }
  }
  % loop over labels
  _for i (0, length(s.camera_data.labels)/3-1, 1) {
    pl.xylabel(
      dotprod(s.camera_data.labels[3*i], s.camera_data.cx),
      dotprod(s.camera_data.labels[3*i], s.camera_data.cy),
      s.camera_data.labels[3*i+1], __push_array(s.camera_data.labels[3*i+2]);;
      s.camera_data.labels_qualifiers[i]
    );
  }
}

% new render function
private define _xfig_camera_render(s, file) {
  % first render all polygons
  s.camera_render_polygons(s, s);
  % default xfig render
  (@(s.camera_data.camera_xfig_render))(file);
}

% return an xfig_plot_new with a camera object included
define xfig_new_camera_plot() {
  variable args = __pop_args(_NARGS);
  variable s = struct_combine(
    struct {
      camera_setup = &_xfig_camera_setup,
      camera_plot_polygon = &_xfig_camera_plot_polygon,
      camera_xyzlabel = &_xfig_camera_xyzlabel,
      camera_shade_region = &_xfig_camera_shade_region,
      camera_render_polygons = &_xfig_camera_render_polygons,
      camera_data = struct { % camera data
	polygons = list_new, % list of polygons (Vector_Type[]) to plot
	polygons_qualifiers = list_new, % plot qualifiers for each polygon
	labels = list_new, % list of labels (Vector_Type[], String_Type)
	labels_qualifiers = list_new, % qualifiers for each label
	incl, zrot, roll, % camera inclination (around x), rotation (around z), and roll (around the optical axis)
	cx, cy, % unit vectors
        camera_xfig_render % remember xfig renderer function
      }
    },
    xfig_plot_new(__push_args(args))
  );
  % default camera setup
  s.camera_setup(0, 0, 0);
  % remember xfig renderer function and then overwrite
  s.camera_data.camera_xfig_render = s.render;
  s.render = &_xfig_camera_render;
  
  return s;
}

%}}}

%%% useful functions %{{{

% function to split a closed line given as an array of vectors using indices.
% ensure that the returned arrays of vectors define a line without breaks
define vecsplitsort(r, n) {
  variable len = vector_norm(vector(diff(r.x[n]), diff(r.y[n]), diff(r.z[n])));
  variable i = @n;
  if (max(len) > 2*median(len)) {
    i = shift(n, where_max(len)+1);
  }
  return vector(r.x[i], r.y[i], r.z[i]);
}

% function to shift, incline, and rotate a vector into the orbital plane
variable a, incl, omega, nOrb, ecc;
define vec2orbit(x) {
  % translate according to the focal point (center of mass)
  ifnot (qualifier_exists("notrans")) {
    x += vector(-sqrt(a^2 - (a*(1-ecc))^2), 0, 0);
  }
  % incline
  ifnot (qualifier_exists("noincl")) {
    x = vector_rotate(x, vector(1, 0, 0), incl * PI/180);
  }
  % rotate
  ifnot (qualifier_exists("noomega")) {
    x = vector_rotate(
      x, nOrb, omega * PI/180
    );
  }
  return x;
}

% calculates an arch between the vectors v1 and v2 with radius r
define arch(v1, v2, r) {
  v1 *= (1./vector_norm(v1));
  v2 *= (1./vector_norm(v2));
  % angle between the vectors and rotation axis, i.e, the normal
  variable angle = acos(dotprod(v1, v2));
  variable axis = crossprod(v1, v2);
  axis *= (1./vector_norm(axis));
  if (qualifier_exists("reverse")) {
    axis *= -1;
    angle = 2*PI - angle;
  }
  % calculate arch by rotating v1 around the axis
  variable nphi = int(1000*angle/2/PI);
  variable step = angle / nphi;
  variable arch = Vector_Type[nphi];
  variable i;
  _for i (0, nphi-1, 1) {
    arch[i] = r*vector_rotate(v1, axis, step*i);
  }
  return merge_struct_arrays(arch);
}

%}}}

%%% define geometry %{{{

% orbit parameters
variable ecc = .05, a = 300; % = 1 - b/a
variable omega = -50, incl = 30.;
% Be disk parameters
variable inclDisk = -50;
variable omegaDisk = 180+28;
variable radDisk = 150;
% neutron star's orbital plase
variable phiNS = .9;

% define normal vectors of the reference frame (plotted later)
% (note that x and y are flipped, see abow)
variable ex = vector(0,1,0);
variable ey = vector(1,0,0);
variable ez = vector(0,0,1);

%}}}

variable n, m;
%%% calculation of orbit, disk, and neutron star position and disk %{{{

% calculate orbit
variable nOrb = vector_rotate(vector(0, 0, 1), vector(1, 0, 0), incl * PI/180);
variable phi = [0:2*PI:#1000];
variable rOrb = vector(
  Double_Type[length(phi)], Double_Type[length(phi)], Double_Type[length(phi)]
);
(rOrb.x, rOrb.y) = ellipse(a, a*(1-ecc), 0, phi);
rOrb = vec2orbit(rOrb);

% calculate Be disk
variable rDisk = vector(
  Double_Type[length(phi)], Double_Type[length(phi)], Double_Type[length(phi)]
);
(rDisk.x, rDisk.y) = ellipse(radDisk, radDisk, 0, phi);
rDisk = vector_rotate(rDisk, vector(1, 0, 0), (incl+inclDisk) * PI/180);
rDisk = vector_rotate(rDisk, nOrb, omegaDisk * PI/180);
% disk normal
variable nDisk = vector_rotate(vector(0, 0, 1), vector(1, 0, 0), (incl+inclDisk) * PI/180);
nDisk = vector_rotate(nDisk, nOrb, omegaDisk * PI/180);

% neutron star position
variable n = wherefirstmin(abs(phi-phiNS*2*PI)); % orbital phase
variable rNS = vector(rOrb.x[n], rOrb.y[n], rOrb.z[n]);

%}}}

variable H = 12; % plot heights (width set individually)
%%% first xfig plot %{{{

variable pl1 = xfig_new_camera_plot(8.,H);
pl1.camera_setup(40, 40, 0);
variable xmin = -315, ymin = -350, wlen = 850;
variable WH = 1.*pl1.plot_data.plot_height/pl1.plot_data.plot_width;
pl1.world(xmin, xmin+wlen/WH, ymin, ymin+wlen);
pl1.axes(; major = 0, minor = 0, color = "white");
pl1.xylabel(.01, .99, "a)", -.5, .5; size = "small", world0);
% define colors
variable orbColor = "#ffca57";
variable tgColor = "#ffff71";
% xyz-axes
variable xyzlen = 250.; % arrow length
pl1.camera_plot_polygon(xyzlen*ex; forward_arrow, color = "red", depth = 20);
pl1.camera_plot_polygon(xyzlen*ey; forward_arrow, color = "red", depth = 20);
pl1.camera_plot_polygon(xyzlen*ez; forward_arrow, color = "red", line = 2);
pl1.camera_xyzlabel(1.05*xyzlen*ex, "x"; color = "red");
pl1.camera_xyzlabel(1.05*xyzlen*ey, "y"; color = "red");
pl1.camera_xyzlabel(1.05*xyzlen*ez, "z"; color = "red");
% plot orbit
n = where(rOrb.y < 0, &m);
pl1.camera_plot_polygon(vecsplitsort(rOrb, n); depth = 85);
pl1.camera_plot_polygon(vecsplitsort(rOrb, m); line = 2, depth = 85);
pl1.camera_shade_region(vecsplitsort(rOrb, n); color = orbColor, depth = 85);
pl1.camera_shade_region(vecsplitsort(rOrb, m); color = orbColor, depth = 95);
n = struct_filter(rOrb, int(length(rOrb.x)*.38); copy);
pl1.camera_xyzlabel(n, "orbital plane"R, .3, .2; size = "small", rotate = -25);
% plot tangent plane of the sky
variable tg = vector(
  -390*[1,0,0,1,1] + 320*[0,1,1,0,0],
  -250*[1,1,0,0,1] + 370*[0,0,1,1,0],
  [0,0,0,0,0]
);
pl1.camera_plot_polygon(tg; depth = 90);
pl1.camera_shade_region(tg; color = tgColor, depth = 90);
n = -28;
pl1.camera_xyzlabel(struct_filter(tg, 1;  copy), "tangent plane"R, .55, -.7; size = "small", rotate = n);
pl1.camera_xyzlabel(struct_filter(tg, 1;  copy), "of the sky"R, .6, -.2; size = "small", rotate = n);
% intersection of the planes
n = wherefirstmin(abs(rOrb.y + rOrb.z));
pl1.camera_plot_polygon(vector(rOrb.x[n], 0, 0); line = 1);
% inclination angle
  % find intersection of the orbit with the x-axis
n = where_min(abs(abs(rOrb.y) + rOrb.z)) + [-1,0,1];
m = interpol_points(0, rOrb.y[n], rOrb.x[n]);
pl1.camera_plot_polygon(vector([m,m], [0,-80], [0,0]); depth = 50);
pl1.camera_xyzlabel(vector(m, -60, 0), "$i$", .75, -.1);
  % find the point on the orbit, which at a certain distance from this intersection point
n = where(rOrb.y < 0 and rOrb.x > 0);
n = n[where_min(abs(vector_norm(struct_filter(rOrb, n; copy) - vector(m, 0, 0)) - 80))];
  % connect the intersection point and the orbit with an arch of the same length as the distance
pl1.camera_plot_polygon(vector(m, 0, 0) + arch(
    vector(0, -1, 0), vector(rOrb.x[n] - m, rOrb.y[n], rOrb.z[n]), 80
));
% periastron and apastron position
variable pstrn = vec2orbit(vector(a, 0, 0));
variable astrn = vec2orbit(vector(-a, 0, 0));
pl1.camera_plot_polygon(merge_struct_arrays([pstrn, astrn]); line = 1, depth = 50);
pl1.camera_xyzlabel(pstrn, "P", -.5, .5);
pl1.camera_xyzlabel(astrn, "A", .3, -.8);
% prism supporting the 3D position of the periastron 
pl1.camera_plot_polygon(merge_struct_arrays([pstrn, pstrn-vector(0,pstrn.y,0)]));
pl1.camera_plot_polygon(merge_struct_arrays([vector(pstrn.x,0,pstrn.z), vector(pstrn.x,0,0)]));
pl1.camera_plot_polygon(vector(pstrn.x, 0, pstrn.z));
% same for the apastron
pl1.camera_plot_polygon(merge_struct_arrays([astrn, astrn-vector(0,astrn.y,0)]); line = 2);
pl1.camera_plot_polygon(merge_struct_arrays([vector(astrn.x,0,astrn.z), vector(astrn.x,0,0)]); line = 2);
pl1.camera_plot_polygon(vector(astrn.x, 0, astrn.z); line = 2);
% omega angle
n = arch(vector(1, 0, 0), pstrn, 85);
m = length(n.x)/2; % vector to half of the arch (-> label)
pl1.camera_plot_polygon(n; line = 1);
pl1.camera_xyzlabel(.8*vector(n.x[m], n.y[m], n.z[m]), "$\omega$"R, 0, -.4);
% neutrons star position
pl1.camera_plot_polygon(rNS; forward_arrow, line = 1);
pl1.camera_xyzlabel(.5*rNS, "$\mathbfit{r}_\mathrm{ns}$"R, -.6, .5);
n = wherefirstmin(vector_norm(rOrb - rNS));
pl1.camera_plot_polygon(struct_filter(rOrb, n + int(.05*length(rOrb.x)) + [0,1]; copy); forward_arrow);
% neutron star position projected into the Be disk reference frame
pl1.camera_plot_polygon(rNS; sym = "circle", fill, size = .5, skiporigin);
variable rNSdiskZ = nDisk * dotprod(rNS, nDisk);
pl1.camera_plot_polygon(rNS-rNSdiskZ; forward_arrow, line = 3);
pl1.camera_plot_polygon(merge_struct_arrays([rNS-rNSdiskZ, rNS]); forward_arrow);
pl1.camera_xyzlabel(rNS-.5*rNSdiskZ, "$h\mathbfit{n}_\mathrm{disk}$"R, .6, -.2; rotate = -55);
pl1.camera_xyzlabel(.5*(rNS-rNSdiskZ), "$r\mathbfit{e}_\mathrm{r}$"R, .5, -.8);
% line of sight
pl1.camera_plot_polygon(rNS - vector([0,0], [0,0], [0,230]); color = "blue", forward_arrow);
pl1.camera_xyzlabel(rNS, "line of sight"R, .85, .6; color = "blue", size = "\small", rotate = 37);
pl1.camera_xyzlabel(rNS, "to Earth"R, .85, 1.2; color = "blue", size = "\small", rotate = 37);

%}}}

%%% second xfig plot %{{{

variable pl2 = xfig_new_camera_plot(10,H);
variable incCam = 20; % camera inclination with respect to the orbital plane
pl2.camera_setup(incl-90+incCam, 0, 0); % incl-90 -> edge on
% rotate the camera around the orbital normal
variable rotCam = 160;
pl2.camera_data.cx = vector_rotate(pl2.camera_data.cx, nOrb, rotCam*PI/180);
pl2.camera_data.cy = vector_rotate(pl2.camera_data.cy, nOrb, rotCam*PI/180);
variable xmin = -260, ymin = -270, wlen = 500;
variable WH = 1.*pl2.plot_data.plot_height/pl2.plot_data.plot_width;
pl2.world(xmin, xmin+wlen/WH, ymin, ymin+wlen);
pl2.axes(; major = 0, minor = 0, color = "white");
pl2.xylabel(.05, .87, "b)", -.5, .5; size = "small", world0);
xyzlen = 200;
pl2.camera_plot_polygon(xyzlen*ez; forward_arrow, color = "red", line = 2);
pl2.camera_xyzlabel(1.05*xyzlen*ez, "z"; color = "red");
% define colors
variable diskColor = "skyblue";
% z-axis projected onto the orbital plane
variable zdisk = xyzlen*(ez - (ez*nOrb)*nOrb);
%zdisk *= (1./vector_norm(zdisk));
pl2.camera_plot_polygon(zdisk; color = "red", line = 1);
pl2.camera_plot_polygon(merge_struct_arrays([xyzlen*ez, zdisk]); line = 2, color = "red");
% plot orbit
pl2.camera_plot_polygon(rOrb; depth = 75);
pl2.camera_shade_region(rOrb; color = orbColor, depth = 100);
n = where(.837 < phi/2/PI < .95); % nasty hack for the dotted line behin the Be disk
pl2.camera_plot_polygon(struct_filter(rOrb, n; copy); depth = 65, line = 2);
n = struct_filter(rOrb, int(length(rOrb.x)*.21); copy);
pl2.camera_xyzlabel(n, "orbital plane"R, 0, -.3; size = "small", rotate = -19);
pl2.camera_xyzlabel(pstrn, "P", .5, -.5);
% plot Be disk
n = where(dotprod(rDisk, nOrb) < 0, &m);
pl2.camera_plot_polygon(vecsplitsort(rDisk, n); depth = 70);
pl2.camera_plot_polygon(vecsplitsort(rDisk, m); line = 2, depth = 85);
pl2.camera_shade_region(vecsplitsort(rDisk, n); color = diskColor, depth = 70);
pl2.camera_shade_region(vecsplitsort(rDisk, m); color = diskColor, depth = 105);
n = struct_filter(rDisk, int(length(rDisk.x)*.15); copy);
pl2.camera_xyzlabel(n, "Be disk"R, 0, .5; size = "small", rotate = -23);
% highest point of the disk above the orbit
variable hline = vector_rotate(vector(0, 1, 0), vector(1, 0, 0), (incl+inclDisk)*PI/180);
hline = radDisk*vector_rotate(hline, nOrb, omegaDisk*PI/180);
pl2.camera_plot_polygon(hline; line = 3);
pl2.camera_xyzlabel(hline*1.1, "H");
pl2.camera_plot_polygon(hline - (hline*nOrb)*nOrb; line = 1);
pl2.camera_plot_polygon(merge_struct_arrays([hline, hline - (hline*nOrb)*nOrb]); line = 2);
% omega disk
n = arch(zdisk, hline - (hline*nOrb)*nOrb, 40; reverse);
pl2.camera_plot_polygon(n; line = 1);
pl2.camera_xyzlabel(.5*struct_filter(n, length(n.x)/2-1; copy), "$\theta$"R, 0, .1);
% disk inclination
n = arch(hline, hline - (hline*nOrb)*nOrb, 60);
pl2.camera_plot_polygon(n; line = 2);
pl2.camera_xyzlabel(.7*struct_filter(n, length(n.x)/2-1; copy), "$\delta$"R, .2, -.2);
% neutrons star position (new one compared to plot 1)
phiNS = .09;
n = wherefirstmin(abs(phi-phiNS*2*PI)); % orbital phase
rNS = vector(rOrb.x[n], rOrb.y[n], rOrb.z[n]);
pl2.camera_plot_polygon(rNS; sym = "circle", fill, size = .5, skiporigin);
pl2.camera_plot_polygon(rNS; forward_arrow, line = 1);
pl2.camera_xyzlabel(.6*rNS, "$\mathbfit{r}_\mathrm{ns}$"R, 1.1, .9);
n = wherefirstmin(vector_norm(rOrb - rNS));
pl2.camera_plot_polygon(struct_filter(rOrb, n + int(.05*length(rOrb.x)) + [0,1]; copy); forward_arrow);
% neutron star position projected into the Be disk reference frame
rNSdiskZ = nDisk * dotprod(rNS, nDisk);
pl2.camera_plot_polygon(rNS-rNSdiskZ; forward_arrow, line = 3);
pl2.camera_plot_polygon(merge_struct_arrays([rNS-rNSdiskZ, rNS]); forward_arrow);
pl2.camera_xyzlabel(rNS-.5*rNSdiskZ, "$h\mathbfit{n}_\mathrm{disk}$"R, 0, -.3; rotate = 39);
pl2.camera_xyzlabel(.9*(rNS-rNSdiskZ), "$r\mathbfit{e}_\mathrm{r}$"R, 0, -.7);

%}}}

% combine and render
% (note: the camera plot renderes the lines only when .render is called.
%        thus we need to call these first, which is not a convenient way...)
pl1.render("../plots/reference_frames.pdf");
pl2.render("../plots/reference_frames.pdf");
xfig_new_hbox_compound(pl1,pl2).render("../plots/reference_frames.pdf");