Difference between revisions of "Isis tutorial gratings"
| (One intermediate revision by one other user not shown) | |||
| Line 177: | Line 177: | ||
Since we do not have an ARF and RMF for the other orders, we need to tell isis not to work with these data sets: | Since we do not have an ARF and RMF for the other orders, we need to tell isis not to work with these data sets: | ||
<pre> | <pre> | ||
| − | isis> exclude([capella[0],capella[1],capella[4],capella[5]); | + | isis> exclude([capella[0],capella[1],capella[4],capella[5]]); |
</pre> | </pre> | ||
The argument of the <code>exclude</code> function is an array containing the indices of all spectra that should be ignored when fitting. In slang/isis, arrays are defined by listing their contents in brackets, i.e., | The argument of the <code>exclude</code> function is an array containing the indices of all spectra that should be ignored when fitting. In slang/isis, arrays are defined by listing their contents in brackets, i.e., | ||
| Line 221: | Line 221: | ||
[[File:Gratings03.png|center]] | [[File:Gratings03.png|center]] | ||
| − | All three lines can be clearly seen in the data set. In order to get more quantitative information, a look at the spectral plot indicates that we should be able to model this spectral region well with a spectral model that consists of the three lines plus a constant flux component (model name <code>constant</code>) that describes the continuum emission. We should probably also ignore the 20.5-21.5 A band because otherwise the fit would be contaminated by the emission lines there. Finally, experience tells us that in such line fits it is often not a good idea to let the wavelength/energy of the line to be completely free. The reason is that often initially the < | + | All three lines can be clearly seen in the data set. In order to get more quantitative information, a look at the spectral plot indicates that we should be able to model this spectral region well with a spectral model that consists of the three lines plus a constant flux component (model name <code>constant</code>) that describes the continuum emission. We should probably also ignore the 20.5-21.5 A band because otherwise the fit would be contaminated by the emission lines there. Finally, experience tells us that in such line fits it is often not a good idea to let the wavelength/energy of the line to be completely free. The reason is that often initially the <math>\chi^2</math>-minimization routine will be trying to change the wavelength by a large factor and as a result it could be that the lines are switched. We therefore allow the lines only to vary by 0.1 A around their official values. |
With the commands discussed in the walkthrough, and with the information given by <code>help set_par</code> you should now be able to setup a fit function that looks like this (note: the <code>gauss</code>-model in isis is a Gaussian line in Angstrom units, the <code>gaussian</code>-model is the same, but in keV units): | With the commands discussed in the walkthrough, and with the information given by <code>help set_par</code> you should now be able to setup a fit function that looks like this (note: the <code>gauss</code>-model in isis is a Gaussian line in Angstrom units, the <code>gaussian</code>-model is the same, but in keV units): | ||
| Line 286: | Line 286: | ||
and the residuals are flat. This is not surprising, given that the reduced chi-square of the fit was only 0.5. | and the residuals are flat. This is not surprising, given that the reduced chi-square of the fit was only 0.5. | ||
| − | Looking at the paper by Ness et al., for the spectral diagnosis the ratio < | + | Looking at the paper by Ness et al., for the spectral diagnosis the ratio <math>G=(f+i)/r</math> as well as the ratio <math>R=f/i</math> is used. As discussed by Ness et al., the diagnostic information contained in these ratios is discussed in great detail by [http://adsabs.harvard.edu/abs/2001A%26A...376.1113P Porquet et al. (2001)] (where the resonance line is called w, the intercombination x+y, and the forbidden line z; sorry, nobody claimed scientists are consistent...). Porquet et al. (2001) show that R is mainly dependent on the electron density and G is mainly dependent on the temperature. |
The following analysis can now proceed either by using your pocket calculator or by using isis as a pocket calculator. Since we have not yet introduced programming in slang/isis, feel free to use either way, or [isis:tutorial:slang take a look at our Slang programming introduction]. In the following, we show how one would get about calculating the above ratios with isis. To understand the code, you need to know that in slang structures contain several named values and that you can access the one of the variables ("tags") that make up the content of a structure with the usual <code>variable.tag</code> syntax that is also used, e.g., in C. Furthermore, read the help for the isis <code>get_params</code> function<ref>if one is just interested in the best fit value of a parameter, you can also use the <code>get_par</code> function, however, this would not have allowed us to introduce slang structures...</ref>. | The following analysis can now proceed either by using your pocket calculator or by using isis as a pocket calculator. Since we have not yet introduced programming in slang/isis, feel free to use either way, or [isis:tutorial:slang take a look at our Slang programming introduction]. In the following, we show how one would get about calculating the above ratios with isis. To understand the code, you need to know that in slang structures contain several named values and that you can access the one of the variables ("tags") that make up the content of a structure with the usual <code>variable.tag</code> syntax that is also used, e.g., in C. Furthermore, read the help for the isis <code>get_params</code> function<ref>if one is just interested in the best fit value of a parameter, you can also use the <code>get_par</code> function, however, this would not have allowed us to introduce slang structures...</ref>. | ||
| Line 312: | Line 312: | ||
Per the discussion in Porquet, the small value of G is an indication that the observed plasma is dominated by collisions, i.e., it is very thin and very hot and the ionization of the plasma is due to collisions and not due to a strong X-ray source in the vicinity that ionizes the plasma through photoionization. We are also happy that our ratio for R, 4.7, is close to that found by Ness et al., which is around 4 (right hand panel of their Figure 10). | Per the discussion in Porquet, the small value of G is an indication that the observed plasma is dominated by collisions, i.e., it is very thin and very hot and the ionization of the plasma is due to collisions and not due to a strong X-ray source in the vicinity that ionizes the plasma through photoionization. We are also happy that our ratio for R, 4.7, is close to that found by Ness et al., which is around 4 (right hand panel of their Figure 10). | ||
| − | While this is all very nice and the result that we obtain is in rough agreement with the literature, we do not know how uncertain our parameters are. The reason is that even though we have the best fit, we do not yet know the uncertainty of our fit parameters. To calculate the uncertainty of a parameter isis uses the usual < | + | While this is all very nice and the result that we obtain is in rough agreement with the literature, we do not know how uncertain our parameters are. The reason is that even though we have the best fit, we do not yet know the uncertainty of our fit parameters. To calculate the uncertainty of a parameter isis uses the usual <math>\Delta\chi^2</math> approach, first discussed for X-ray astronomical data by [http://adsabs.harvard.edu/abs/1976ApJ...208..177L Lampton, Margon, Bowyer, 1978, Apj 208, 177]. We will call the parameter for which the uncertainty is to be calculated the "parameter of interest". Lampton et al. show that the confidence interval can be determined with the following recipe: |
| − | # Calculate < | + | # Calculate <math>\Delta\chi^2</math> from the chi-square-distribution with one degree of freedom. Common in X-ray astronomy are "<math>1\sigma</math>"-errors with <math>\Delta\chi^2=1.00</math>, 90% confidence ranges with <math>\Delta\chi^2=2.71</math>, and 99% confidence contours with <math>\Delta\chi^2=6.63</math>. The most common errors are the 90% ones. |
| − | # Change the parameter of interest away from its best fit value to a slightly smaller value. Keep it frozen and refit. This will result in a slightly larger < | + | # Change the parameter of interest away from its best fit value to a slightly smaller value. Keep it frozen and refit. This will result in a slightly larger <math>\chi^2</math> for the best fit. |
| − | # Repeat the previous step until you find the parameter value where the chi-squared is < | + | # Repeat the previous step until you find the parameter value where the chi-squared is <math>\chi^2 = \chi_\mathrm{min}^2+\Delta\chi^2</math> where <math>\chi_\mathrm{min}^2</math> is the chi-squared of our original best fit. The value of our parameter is now the lower bound of the confidence interval. |
# Repeat for values larger than the best fit value until you find the upper bound of the confidence region. | # Repeat for values larger than the best fit value until you find the upper bound of the confidence region. | ||
| − | # Designating the lower and upper end of the confidence region by < | + | # Designating the lower and upper end of the confidence region by <math>p_\mathrm{min}</math> and <math>p_\mathrm{max}</math> and the best fit value <math>p</math>, we then write the best fit parameter as follows: <math>p^{+\Delta p_\mathrm{max}}_{-\Delta p_\mathrm{min}}</math> where <math>\Delta p_\mathrm{max} = p_\mathrm{max}-p</math> and <math>p_\mathrm{min}=p-p_\mathrm{min}</math>. |
| − | Because of correlations between parameters, error bars are typically not symmetric and great care has to be taken when doing error propagation. We ignore all of those for the moment and use the rule of thumb that if the error bars are not too asymmetric, a rough estimate for a symmetric error bar which can be used for the standard Gaussian error propagation is the average of the lower and the upper error bars, i.e., use < | + | Because of correlations between parameters, error bars are typically not symmetric and great care has to be taken when doing error propagation. We ignore all of those for the moment and use the rule of thumb that if the error bars are not too asymmetric, a rough estimate for a symmetric error bar which can be used for the standard Gaussian error propagation is the average of the lower and the upper error bars, i.e., use <math>\Delta p =(\Delta p_\mathrm{min}+\Delta p_\mathrm{max})/2</math> and write the best fit parameter as <math>p\pm\Delta p</math> (where we usually also use 90% error bars!). |
The above procedure is implemented in isis through the <code>conf</code> and <code>vconf</code> functions. These are identical, <code>vconf</code> gives more information about the procedure (the "v" stands for "verbose"). Since the above procedure searches for the zero of a function, it is not guaranteed to converge numerically. For this reason isis calculates confidence intervals only when explicit limits are set. These limits are returned in case the error calculation failed. Typically, for good data sets the errors will be less than 20-30% of the value, but this depends a lot on the data set and one often has to play around a little bit. | The above procedure is implemented in isis through the <code>conf</code> and <code>vconf</code> functions. These are identical, <code>vconf</code> gives more information about the procedure (the "v" stands for "verbose"). Since the above procedure searches for the zero of a function, it is not guaranteed to converge numerically. For this reason isis calculates confidence intervals only when explicit limits are set. These limits are returned in case the error calculation failed. Typically, for good data sets the errors will be less than 20-30% of the value, but this depends a lot on the data set and one often has to play around a little bit. | ||
| Line 358: | Line 358: | ||
0.0008692617403948057 | 0.0008692617403948057 | ||
</pre> | </pre> | ||
| − | this means that the error bar is almost symmetric and therefore < | + | this means that the error bar is almost symmetric and therefore <math>f=(8.7\pm1.0)\times10^{-5}\,\mathrm{ph}\,\mathrm{s}^{-1}\,\mathrm{cm}^{-2}</math> |
'''''Exercise 4''''' | '''''Exercise 4''''' | ||
Revision as of 11:34, 3 April 2022
Further Data Fitting
The walk through isis has given you a first overview of a simple X-ray spectral analysis. In this part of the tutorial we build upon this experience by performing a more complicated analysis of Chandra gratings spectra. You will learn about X-ray data archives and what to do when not all keywords are set in a X-ray spectral file. Furthermore we introduce an important X-ray diagnostics for tenuous plasmas.
Data Archives and the ADS
ADS
In this tutorial we will demonstrate the analysis of Chandra gratings data of stellar spectra and try to reproduce the results obtained by Jan-Uwe Ness et al., 2002, Coronal density diagnostics with Helium-like triplets: CHANDRA-LETGS observations of Algol, Capella, Procyon, epsilon Eri, alpha Cen A&B, UX Ari, AD Leo, YY Gem, and HR 1099, Astronomy and Astrophysics 394, 911.
Exercise 1
- Go to the ADS Abstract Service and search for the above paper. The best way to do this is to enter
^Nessfor the Author andCapellafor the Object. The ADS is the best data base to find astronomical literature. It goes back to the early 1800s and is almost complete for the past 50 years or so. It will be very worth your time to familiarize yourself with searching papers there - even if you do not want to do astronomy in the end but other areas of physics, which are indexed in the ADS as well. In order to make sure that you really did the search and did not just click the link above, what is the newest paper published by this author?
- Download, print, and read this paper. Yes, really, print it - you will need to refer to this paper often and you might want to scribble comments on your paper copy and you will read the paper much more intensively if it is not on a computer screen. In order to get to the PDF-copy of the paper, click on "Full Refereed Journal Article (PDF/Postscript)" in the above link. You will see it is colored in green, meaning that the paper is not behind a paywall. This is not the case for new articles, unfortunately, in this case you can always go to the arXiv-Link and get a preprint from there. Virtually all important astronomical papers can be found this way.
Data Archives
Here, we will show you how to perform the analysis of Capella, in your homework you will work on one of the other sources. Like the analysis of data from all other X-ray satellites, the reduction of Chandra gratings data can become very involved. Since we "just" want to analyze the time averaged spectrum of the source, we are lucky that somebody else (well, the Chandra gratings team) has done the work for us and has put the reduced spectra on the WWW for us. Such archives of pre-reduced data exist for all satellites, and while I caution not to use the reduced data in these archives for publication-level work, they are useful to get a feel for what is available (the reason why you do not want to use these data for publication level work is that you will typically have to apply a newer version of the detector calibration, different background screening criteria, different time intervals, and so on). The following list contains the most important X-ray astronomical archives:
- TO BE WRITTEN
- TGCat contains all public observations performed with the Chandra transmission gratings spectrometers. The user interface is self-explanatory and there is a nice help section available. If you know the name of the object you're interested in, enter it in the "Quick Query" box, then click on the object name and you will be getting a list of all available observations.
Exercise 2
- Download the observation with the longest exposure time available for the object you are interested in, unless your instructions say otherwise. If possible, disregard the observations where the HRC was in the focal plane, i.e., look at the ACIS-observations only (the HRC is not energy dispersive, and therefore order sorting is not so easy with this detector).
Select the data, ask TGCat to send you an email, and then download the file. For example
wget http://tgcat.mit.edu/tmp/1337349938_174950000/tgcat.tar.gz
Unpack it with
tar xzvf tgcat.tar.gz
For Capella, we download the data from observation ID 8319. The data set looks as follows:
hde226868:~/isistut> cd tgcat hde226868:~/isistut/tgcat> ls -l total 16 drwxr-xr-x 3 wilms wilms 4096 May 18 16:05 . drwxr-xr-x 3 wilms wilms 4096 May 20 14:05 .. -rw-r--r-- 1 wilms wilms 327 May 18 16:05 checksums.dat drwxr-xr-x 2 wilms wilms 4096 May 18 16:05 obs_8319_tgid_3283 hde226868:~/isistut/tgcat> cd obs_8319_tgid_3283 hde226868:~/isistut/tgcat/obs_8319_tgid_3283> ls -l total 15648 -r--r--r-- 1 wilms wilms 1419840 May 18 16:05 pha2.gz -r--r--r-- 1 wilms wilms 256320 May 18 16:05 leg_-1.arf -r--r--r-- 1 wilms wilms 7030080 May 18 16:05 leg_-1.rmf -r--r--r-- 1 wilms wilms 256320 May 18 16:05 leg_1.arf -r--r--r-- 1 wilms wilms 7032960 May 18 16:05 leg_1.rmf -rw-r--r-- 1 wilms wilms 71 May 18 16:05 vv_report.txt
The spectral file is called pha2.gz, which is not a very meaningful name, so we unpack it and rename it:
hde226868:~/isistut/tgcat/obs_8319_tgid_3283> gunzip pha2.gz hde226868:~/isistut/tgcat/obs_8319_tgid_3283> mv pha2 capella.pha2
Note the name pha2. In the walkthrough we encountered PHA-files, which contain one spectrum. pha2-files contain multiple spectra. They are used, for example, in pulse phase resolved spectroscopy of neutron stars or in gratings spectra, where they contain multiple spectra.
Exercise 3
- Take a look at the contents of your pha2-file using
fvandfstruct. Note that each "row" in the pha2-file now contains one spectrum.
Preparing Gratings Data for Fitting
We now enter "isis", load the "isisscripts", and load our data set
hde226868:~/isistut/tgcat/obs_8319_tgid_3283> isis
:
isis> require("isisscripts");
:
isis> capella=load_data("capella.pha2");
Reading: ......
As usual, we first take a look at what has been loaded, this time using a helpful function from the "isisscripts" that lists the data and the loaded "ARF"- and "RMF"-files.:
isis> list_all; Current Spectrum List: id instrument part/m src use/nbins A R totcts exp(ksec) target 1 LETG-ACIS leg-3 1 8192/ 8192 - - 1.0222e+04 59.146 Capella file: capella.pha2 2 LETG-ACIS leg-2 1 8192/ 8192 - - 4.4290e+03 59.146 Capella file: capella.pha2 3 LETG-ACIS leg-1 1 8192/ 8192 - - 7.0583e+04 59.146 Capella file: capella.pha2 4 LETG-ACIS leg+1 1 8192/ 8192 - - 1.1496e+05 59.146 Capella file: capella.pha2 5 LETG-ACIS leg+2 1 8192/ 8192 - - 4.7930e+03 59.146 Capella file: capella.pha2 6 LETG-ACIS leg+3 1 8192/ 8192 - - 6.2380e+03 59.146 Capella file: capella.pha2 isis>
We note two things:
load_dataloaded all contents of thepha2-file, total of six spectra. What these spectra are is identified in thepart/m-column:legis the "low energy grating" of Chandra-HETGS (the other grating would be calledmegformedium energy grating), and -3, -2, -1, +1, +2, +3 identifies the order of the spectrum.- No
ARFandRMFare listed. This means that while the spectra have been loaded we still need to tellisiswhatARFandRMFto use for the spectra (you can also see this by noticing the dashes in theAandRcolumns).
We now remind ourselves what responses and ARF we were provided with, by using isis' "shell escape". This means that within isis we can precede a normal shell command by an exclamation mark to have it executed by the shell:
isis> !ls -l total 15648 -r--r--r-- 1 wilms wilms 1419840 May 18 16:05 capella.pha2 -r--r--r-- 1 wilms wilms 256320 May 18 16:05 leg_-1.arf -r--r--r-- 1 wilms wilms 7030080 May 18 16:05 leg_-1.rmf -r--r--r-- 1 wilms wilms 256320 May 18 16:05 leg_1.arf -r--r--r-- 1 wilms wilms 7032960 May 18 16:05 leg_1.rmf -rw-r--r-- 1 wilms wilms 71 May 18 16:05 vv_report.txt isis>
This means that we only have RMFs and ARFs available for the first order and we will have to ignore the higher orders. This is fine since most photons end up in the 1st order anyway. Let us now load the files:
isis> arfm1=load_arf("leg_-1.arf");
isis> arfp1=load_arf("leg_1.arf");
isis> rmfm1=load_rmf("leg_-1.rmf");
isis> rmfp1=load_rmf("leg_1.rmf");
and check that everything went fine:
isis> list_all; Current Spectrum List: id instrument part/m src use/nbins A R totcts exp(ksec) target 1 LETG-ACIS leg-3 1 8192/ 8192 - - 1.0222e+04 59.146 Capella file: capella.pha2 2 LETG-ACIS leg-2 1 8192/ 8192 - - 4.4290e+03 59.146 Capella file: capella.pha2 3 LETG-ACIS leg-1 1 8192/ 8192 - - 7.0583e+04 59.146 Capella file: capella.pha2 4 LETG-ACIS leg+1 1 8192/ 8192 - - 1.1496e+05 59.146 Capella file: capella.pha2 5 LETG-ACIS leg+2 1 8192/ 8192 - - 4.7930e+03 59.146 Capella file: capella.pha2 6 LETG-ACIS leg+3 1 8192/ 8192 - - 6.2380e+03 59.146 Capella file: capella.pha2 Current RMF List: id grating detector m type file/function 1 LETG ACIS-7 -1 file: leg_-1.rmf 2 LETG ACIS-7 1 file: leg_1.rmf Current ARF List: id grating detector part/m src nbins exp(ksec) target 1 LETG ACIS leg-1 0 8192 59.15 Capella file: leg_-1.arf 2 LETG ACIS leg+1 0 8192 59.15 Capella file: leg_1.arf isis>
We now need to assign each ARF and RMF to the spectrum taken with this detector:
isis> assign_rmf(rmfm1,capella[2]); isis> assign_arf(arfm1,capella[2]); isis> assign_rmf(rmfp1,capella[3]); isis> assign_arf(arfp1,capella[3]);
Note that instead of using the id-values directly (e.g., assign_rmf(1,3)) we use the isis-variables that were returned in the different load-commands (capella is a variable, and in slang/isis arrays are zero-based). This approach is better than using the ids directly since it minimizes the likelihood of typos and we do not have to remember strange id numbers but rather variable names that (should) make sense. If you want to find out more about the slang programming language, you can have a look at the nice documentation at [1]. In this case, especially Chapter 6 (Variables) and 11 (Arrays) might be interesting for you.
Let's check whether the assignment was ok:
isis> list_data; Current Spectrum List: id instrument part/m src use/nbins A R totcts exp(ksec) target 1 LETG-ACIS leg-3 1 8192/ 8192 - - 1.0222e+04 59.146 Capella file: capella.pha2 2 LETG-ACIS leg-2 1 8192/ 8192 - - 4.4290e+03 59.146 Capella file: capella.pha2 3 LETG-ACIS leg-1 1 8192/ 8192 1 1 7.0583e+04 59.146 Capella file: capella.pha2 4 LETG-ACIS leg+1 1 8192/ 8192 2 2 1.1496e+05 59.146 Capella file: capella.pha2 5 LETG-ACIS leg+2 1 8192/ 8192 - - 4.7930e+03 59.146 Capella file: capella.pha2 6 LETG-ACIS leg+3 1 8192/ 8192 - - 6.2380e+03 59.146 Capella file: capella.pha2
Notice that the A and R columns now contain the indices of the respective ARF and RMF.
The First Fit
Since we do not have an ARF and RMF for the other orders, we need to tell isis not to work with these data sets:
isis> exclude([capella[0],capella[1],capella[4],capella[5]]);
The argument of the exclude function is an array containing the indices of all spectra that should be ignored when fitting. In slang/isis, arrays are defined by listing their contents in brackets, i.e.,
array=[1,2,5,6];
It is also possible to use a shorthand notation to define larger arrays, e.g.,
array=[1:10];
creates an array containing the 10 numbers 1,2,...,10, while
array=[1:10:2];
creates an array containing the numbers 1,3,5,...,9. In principle, you can do something like this also with floating point numbers, but because of subtleties with floating point arithmetic, we do not recommend using this feature of the language.
In the exclude-example before, note that we are again listing the indices of the spectra indirectly by specifying them through the capella variable. As before, this makes our code more portable. Finally, note that you could have also used the ignore-function to ignore these data sets, but exclude is preferred since it does not affect the currently noticed energy ranges.
Finally, since we now only have two spectra to work with, let's remember their indices in shorter variables such that we do not have to type capella[x] all the time...
isis> m1=capella[2]; isis> p1=capella[3];
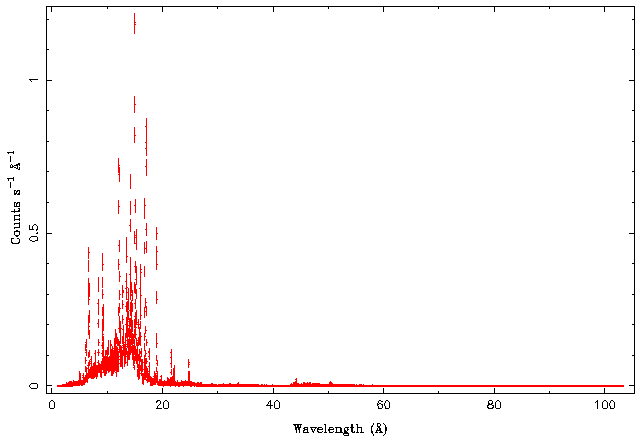
We first plot the whole data set, switching the x-axis unit to Angstroms, because this is more appropriate for gratings data:
isis> fancy_plot_unit("A");
isis> plot_data(p1;dsym=1,dcol=2);
Note that for the moment we are only plotting one data set in order not to confuse ourselves. With dsym=1 we switch off the plot symbol, which is only distracting and does not help in understanding the figure (try the command without the dsym-qualifier!).
The resulting figure looks as follows:
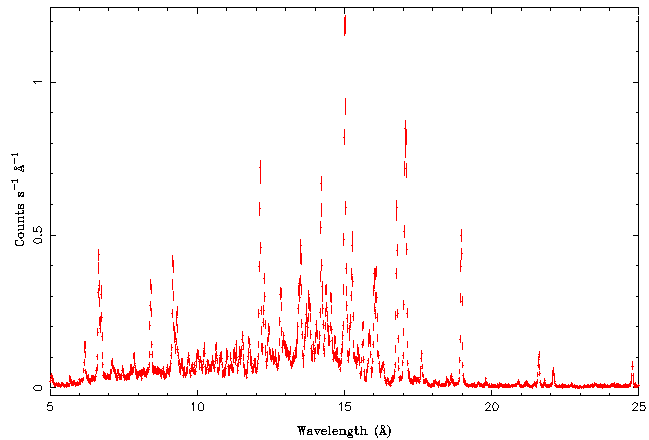
Notice the very strong emission lines, which are typical for stellar coronae. Most of the things are happening between 5 and 25 Angstroms, so let's zoom in that region:
Isis has very powerful functions that help in the identification of these lines. Also note the "bump" at lower wavelengths, which is due to bremsstrahlung emission of the hot corona.
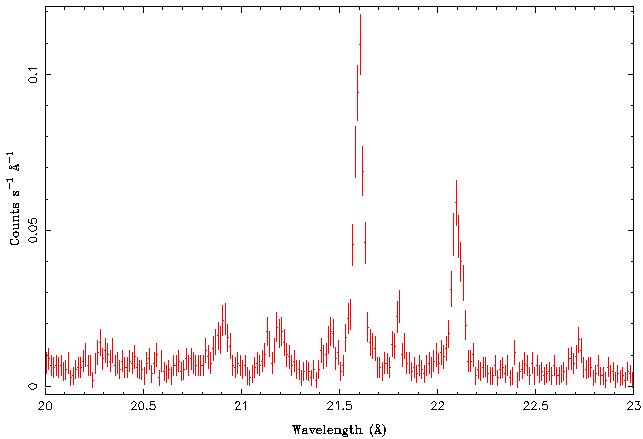
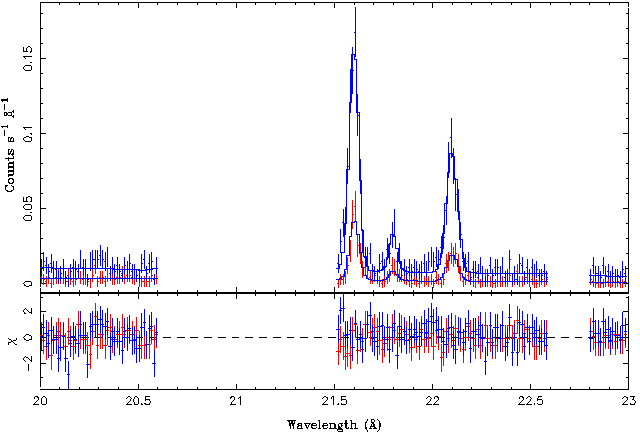
Right now we are only interested in the He-like oxygen triplet at 21.6, 21.8, and 22.1 Angstroms. These are called the resonant, intercombination, and forbidden line, respectively, and their fluxes are typically called r, i, and f. Let's therefore take a look at the 20-23 A band only:
All three lines can be clearly seen in the data set. In order to get more quantitative information, a look at the spectral plot indicates that we should be able to model this spectral region well with a spectral model that consists of the three lines plus a constant flux component (model name constant) that describes the continuum emission. We should probably also ignore the 20.5-21.5 A band because otherwise the fit would be contaminated by the emission lines there. Finally, experience tells us that in such line fits it is often not a good idea to let the wavelength/energy of the line to be completely free. The reason is that often initially the [math]\displaystyle{ \chi^2 }[/math]-minimization routine will be trying to change the wavelength by a large factor and as a result it could be that the lines are switched. We therefore allow the lines only to vary by 0.1 A around their official values.
With the commands discussed in the walkthrough, and with the information given by help set_par you should now be able to setup a fit function that looks like this (note: the gauss-model in isis is a Gaussian line in Angstrom units, the gaussian-model is the same, but in keV units):
isis> list_par; constant(1)+gauss(1)+gauss(2)+gauss(3) idx param tie-to freeze value min max 1 constant(1).factor 0 0 1 0 1e+10 2 gauss(1).area 0 0 1 0 0 photons/s/cm^2 3 gauss(1).center 0 0 21.6 21.5 21.7 A 4 gauss(1).sigma 0 0 0.025 1e-06 1 A 5 gauss(2).area 0 0 1 0 0 photons/s/cm^2 6 gauss(2).center 0 0 21.8 21.7 21.9 A 7 gauss(2).sigma 0 0 0.025 1e-06 1 A 8 gauss(3).area 0 0 1 0 0 photons/s/cm^2 9 gauss(3).center 0 0 22.1 22 22.2 A 10 gauss(3).sigma 0 0 0.025 1e-06 1 A
To get a good fit, plot the model (do not forget the eval_counts command!), and adjust the constant, line widths, and line fluxes (area-parameter) until you get a good "fit by eye". Playing a little bit with the parameters I find a starting model that looks as follows:
We now ignore the 20.6-21.5 and 22.6-22.8 Angstrom bands in both data sets:
isis> ignore([p1,m1],20.6,21.5); isis> ignore([p1,m1],22.6,22.8);
Replot in order to confirm that these data are gone! Furthermore, we also ignore everything below 20A and above 23A:
isis> ignore([p1,m1],NULL,20); isis> ignore([p1,m1],23,NULL);
perform the fit:
isis> Fit_Verbose=1; isis> fit_counts();
The best fit parameters are as follows:
isis> list_par; constant(1)+gauss(1)+gauss(2)+gauss(3) idx param tie-to freeze value min max 1 constant(1).factor 0 0 1.342954e-05 0 1e+10 2 gauss(1).area 0 0 0.001175245 0 0 photons/s/cm^2 3 gauss(1).center 0 0 21.60025 21.5 21.7 A 4 gauss(1).sigma 0 0 0.01614977 1e-06 1 A 5 gauss(2).area 0 0 0.000183689 0 0 photons/s/cm^2 6 gauss(2).center 0 0 21.79914 21.7 21.9 A 7 gauss(2).sigma 0 0 0.0108202 1e-06 1 A 8 gauss(3).area 0 0 0.0008692617 0 0 photons/s/cm^2 9 gauss(3).center 0 0 22.09971 22 22.2 A 10 gauss(3).sigma 0 0 0.02135323 1e-06 1 A
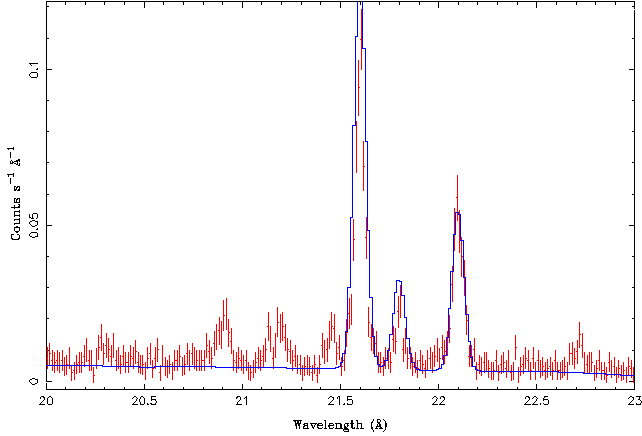
To check whether all went well with the fit, we plot our best fit. While for the manual adjustment of the fit parameters it was sufficient to just look at one of the spectra, we really should look at all of our data. This is done with
isis> plot_data({m1,p1};dsym={1,1},decol={2,4},dcol={2,4},mcol={4,4},res=1);
where the {1,2} etc. are so-called lists. These are somewhat more flexible forms of arrays. We will address the details of this data type later, for the moment, just remember that you need to put everything in curly parentheses instead of brackets. In the above, the color 4 is used for the m=+1 spectrum and 2 for the m=-1 spectrum.
The best fit looks as follows:
and the residuals are flat. This is not surprising, given that the reduced chi-square of the fit was only 0.5.
Looking at the paper by Ness et al., for the spectral diagnosis the ratio [math]\displaystyle{ G=(f+i)/r }[/math] as well as the ratio [math]\displaystyle{ R=f/i }[/math] is used. As discussed by Ness et al., the diagnostic information contained in these ratios is discussed in great detail by Porquet et al. (2001) (where the resonance line is called w, the intercombination x+y, and the forbidden line z; sorry, nobody claimed scientists are consistent...). Porquet et al. (2001) show that R is mainly dependent on the electron density and G is mainly dependent on the temperature.
The following analysis can now proceed either by using your pocket calculator or by using isis as a pocket calculator. Since we have not yet introduced programming in slang/isis, feel free to use either way, or [isis:tutorial:slang take a look at our Slang programming introduction]. In the following, we show how one would get about calculating the above ratios with isis. To understand the code, you need to know that in slang structures contain several named values and that you can access the one of the variables ("tags") that make up the content of a structure with the usual variable.tag syntax that is also used, e.g., in C. Furthermore, read the help for the isis get_params function[1].
To calculate the ratios then do the following:
isis> r=get_params("gauss(1).area");
isis> i=get_params("gauss(2).area");
isis> f=get_params("gauss(3).area");
take a look at the contents of r (which per the documentation of get_params is an array):
isis> print(r);
{name="gauss(1).area", index=2, value=0.0011752452373316315, min=-1.7976931348623157e+308, max=1.7976931348623157e+308, hard_min=-inf, hard_max=inf, step=0.0, relstep=0.0001, freeze=0, tie=NULL, units="photons/s/cm^2", is_a_norm=1, fun=NULL}
and therefore
isis> rat=f[0].value/i[0].value; isis> g=(f[0].value+i[0].value)/r[0].value; isis> print(rat); 4.732248259283046 isis> print(g); 0.8959412576621245 isis>
Per the discussion in Porquet, the small value of G is an indication that the observed plasma is dominated by collisions, i.e., it is very thin and very hot and the ionization of the plasma is due to collisions and not due to a strong X-ray source in the vicinity that ionizes the plasma through photoionization. We are also happy that our ratio for R, 4.7, is close to that found by Ness et al., which is around 4 (right hand panel of their Figure 10).
While this is all very nice and the result that we obtain is in rough agreement with the literature, we do not know how uncertain our parameters are. The reason is that even though we have the best fit, we do not yet know the uncertainty of our fit parameters. To calculate the uncertainty of a parameter isis uses the usual [math]\displaystyle{ \Delta\chi^2 }[/math] approach, first discussed for X-ray astronomical data by Lampton, Margon, Bowyer, 1978, Apj 208, 177. We will call the parameter for which the uncertainty is to be calculated the "parameter of interest". Lampton et al. show that the confidence interval can be determined with the following recipe:
- Calculate [math]\displaystyle{ \Delta\chi^2 }[/math] from the chi-square-distribution with one degree of freedom. Common in X-ray astronomy are "[math]\displaystyle{ 1\sigma }[/math]"-errors with [math]\displaystyle{ \Delta\chi^2=1.00 }[/math], 90% confidence ranges with [math]\displaystyle{ \Delta\chi^2=2.71 }[/math], and 99% confidence contours with [math]\displaystyle{ \Delta\chi^2=6.63 }[/math]. The most common errors are the 90% ones.
- Change the parameter of interest away from its best fit value to a slightly smaller value. Keep it frozen and refit. This will result in a slightly larger [math]\displaystyle{ \chi^2 }[/math] for the best fit.
- Repeat the previous step until you find the parameter value where the chi-squared is [math]\displaystyle{ \chi^2 = \chi_\mathrm{min}^2+\Delta\chi^2 }[/math] where [math]\displaystyle{ \chi_\mathrm{min}^2 }[/math] is the chi-squared of our original best fit. The value of our parameter is now the lower bound of the confidence interval.
- Repeat for values larger than the best fit value until you find the upper bound of the confidence region.
- Designating the lower and upper end of the confidence region by [math]\displaystyle{ p_\mathrm{min} }[/math] and [math]\displaystyle{ p_\mathrm{max} }[/math] and the best fit value [math]\displaystyle{ p }[/math], we then write the best fit parameter as follows: [math]\displaystyle{ p^{+\Delta p_\mathrm{max}}_{-\Delta p_\mathrm{min}} }[/math] where [math]\displaystyle{ \Delta p_\mathrm{max} = p_\mathrm{max}-p }[/math] and [math]\displaystyle{ p_\mathrm{min}=p-p_\mathrm{min} }[/math].
Because of correlations between parameters, error bars are typically not symmetric and great care has to be taken when doing error propagation. We ignore all of those for the moment and use the rule of thumb that if the error bars are not too asymmetric, a rough estimate for a symmetric error bar which can be used for the standard Gaussian error propagation is the average of the lower and the upper error bars, i.e., use [math]\displaystyle{ \Delta p =(\Delta p_\mathrm{min}+\Delta p_\mathrm{max})/2 }[/math] and write the best fit parameter as [math]\displaystyle{ p\pm\Delta p }[/math] (where we usually also use 90% error bars!).
The above procedure is implemented in isis through the conf and vconf functions. These are identical, vconf gives more information about the procedure (the "v" stands for "verbose"). Since the above procedure searches for the zero of a function, it is not guaranteed to converge numerically. For this reason isis calculates confidence intervals only when explicit limits are set. These limits are returned in case the error calculation failed. Typically, for good data sets the errors will be less than 20-30% of the value, but this depends a lot on the data set and one often has to play around a little bit.
The error bar for the flux of the forbidden line is then calculated as follows:
isis> set_par("gauss(3).area",f[0].value,0,0.75*f[0].value,1.25*f[0].value);
isis> list_par;
constant(1)+gauss(1)+gauss(2)+gauss(3)
idx param tie-to freeze value min max
1 constant(1).factor 0 0 1.342954e-05 0 1e+10
2 gauss(1).area 0 0 0.001175245 0 0 photons/s/cm^2
3 gauss(1).center 0 0 21.60025 21.5 21.7 A
4 gauss(1).sigma 0 0 0.01614977 1e-06 1 A
5 gauss(2).area 0 0 0.000183689 0 0 photons/s/cm^2
6 gauss(2).center 0 0 21.79914 21.7 21.9 A
7 gauss(2).sigma 0 0 0.0108202 1e-06 1 A
8 gauss(3).area 0 0 0.0008692617 0.0006519463 0.001086577 photons/s/cm^2
9 gauss(3).center 0 0 22.09971 22 22.2 A
10 gauss(3).sigma 0 0 0.02135323 1e-06 1 A
isis> (fmi,fma)=vconf("gauss(3).area");
:
: lots of output...
:
gauss(3).sigma= 2.25766046e-02
chi-square value converged
par[8]= 9.64711324e-04 stat= 1.5337e+02 dstat= 2.7100e+00
limit found: 9.64711324e-04 dstat= 2.7100e+00
isis> print(fmi);
0.0007743270669346407
isis> print(fma);
0.0009647113237380715
isis> print(f[0].value-fmi);
9.493467346016499e-05
isis> print(fma-f[0].value);
9.544958334326589e-05
isis> print(f[0].value);
0.0008692617403948057
this means that the error bar is almost symmetric and therefore [math]\displaystyle{ f=(8.7\pm1.0)\times10^{-5}\,\mathrm{ph}\,\mathrm{s}^{-1}\,\mathrm{cm}^{-2} }[/math]
Exercise 4
- Perform the above analysis for "your" star. Do not forget to calculate error bars for R and G using error propagation!
- Use the tables of Porquet et al. to estimate the density and temperature of the plasma. Looking at the discussion by Ness et al., what is the systematic error of this analysis?
References
- ↑ if one is just interested in the best fit value of a parameter, you can also use the
get_parfunction, however, this would not have allowed us to introduce slang structures...