Researchers led by PhD student Caroline Collischon in the group of Manami Sasaki at the Remeis Observatory have introduced a new way of describing shapes in the night sky. In their recent paper on “Morphometry on the sphere” published in Communications Physics, they adapted a set of powerful shape descriptors called Minkowski tensors to the spherical surface. This is necessary for analyzing some sets of image data where projection effects would dominate if projected into flat space, such as astronomical and cosmological data distributed over the whole sky.
Image processing often includes looking into shapes and quantifying them in a meaningful way accessible to both humans and machines. This is the case in many fields, from astronomy to life science.
Many tools have been developed for this task, among them Minkowski functionals and their tensorial counterparts, Minkowski tensors. They are powerful and comprehensive shape descriptors, containing all shape information for convex bodies and enough information for non-convex bodies to be useful. They are additive and consequently very useful for pixel images, where one can calculate them from small 2×2 pixel windows.
One representation, the irreducible Minkowski tensors, are particularly handy for characterizing symmetries of a body in a way that is accessible to humans: The usual Cartesian form forces one to deal with many components per tensor that somehow need to be brought into a scalar form. This has only been satisfyingly solved for rank 2 tensors that encode elongation. On the other hand, the irreducible Minkowski tensors boil their respective symmetry information down to one complex number.
The amplitude of a rank s tensor describes the extent of s-fold symmetry and its phase describes the corresponding orientation. An elongated shape will have a large rank 2 amplitude, whereas rank 4 reacts to “square-ness”. The effects of various such amplitudes and phases can be tested in the morphometer, a small browser tool for gaining some intuition with Minkowski tensors.
Previously, the irreducible Minkowski tensors have been used for analyzing regular, flat images. However, some datasets exist on the surface of the sphere, where projection into flat space would distort the shapes. This is famously the case for the Cosmic Microwave Background (CMB). It can be seen in any direction, rendering flat images useless, and it contains small temperature fluctuations that encode information on the early universe. The details of these fluctuations impact which fundamental cosmological models are viable. This means that powerful morphometric tools are needed.
Basic information on, e.g., the size distribution of these fluctuations is given in the power spectrum, but for more extensive analyses more abstract tools such as the three point correlation were used. On the contrary, Minkowski tensors provide local and real-space shape information, but their irreducible form was unavailable on the sphere. They implemented them for the HEALPix scheme commonly used for CMB data and made their code publicly available.
Collischon and her team looked at the data by creating Minkowski maps; images that show the desired Minkowski tensor of the local surroundings of each output pixel. With this technique, masking data is not an issue – Minkowski map pixels with too many masked input pixels are simply marked as masked as well. Smaller masked input areas can be ignored when adding up the shapes for one output pixel. Additionally, local structures only affect local output pixels, creating a straightforward way for the search for local anisotropies.

The creation of a Minkowski map: For the output map, a circular region is chosen and all sections of the underlying shape within are added up (left). As this window moves across the image, a Minkowski map is created. The right side shows Minkowski maps for several rectangles (white) and their corresponding rank 2 anisotropy. Longer rectangles are shown to have higher anisotropy. As the window (red) moves across the shape, it sometimes catches only part of the contour, leading to characteristic patterns.
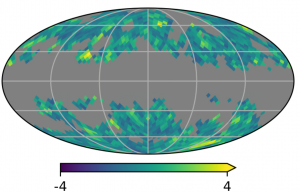
With maps like this, the team tested their methods on Planck CMB temperature data, looking for unusual 2-fold symmetries at length scales of several degrees. They compared Minkowski maps of the data to those of 999 simulations provided by the Planck Collaboration and found two regions where the data appears more anisotropic than the simulations. The origin of these anisotropies is unclear and needs further investigation.
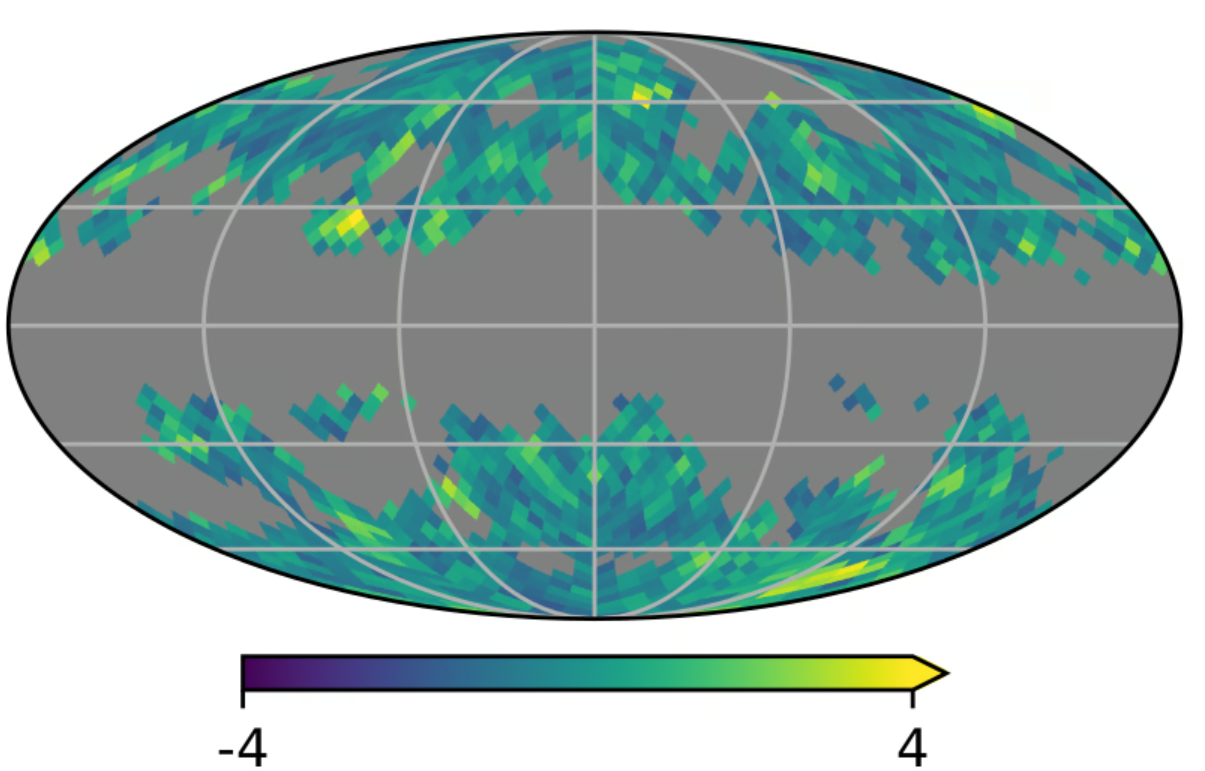
Deviation between Minkowski maps generated for CMB data and simulations in units of standard deviation. Two regions stand out: one near (80, 27), above the Galactic equator to the left, and near (225,-69), to the bottom right.
Furthermore, the scientists checked whether the different tensor ranks provide independent information for such image data, and rank 4 and 2 anisotropies appear uncorrelated for pixels in the simulations. This means that there is more to be learned from such an analysis with higher ranks.
Minkowski tensors thus now enable the scientific community to quantify spherical data in a comprehensive and versatile way, since the necessary tools have been made freely available.
Read more:
Collischon, C., Klatt, M.A., Banday, A.J. et al. Morphometry on the sphere: Cartesian and irreducible Minkowski tensors explained and implemented. Commun Phys 7, 254 (2024).
Caroline Collischon
caroline.collischon@fau.de
+49 9131 85-81016
Manami Sasaki
Manami.Sasaki@fau.de
+49 9131 85-81019