relxill
general information about the model
relxill is a new reflection model, which can
be readily used in common X-ray data analysis tools such as
isis, xspec, or sherpa. It combines the xillver
reflection code (Garcia et al., 2010, 2011, 2013) and the
relline ray tracing
code (Dauser et al., 2010, 2013). The striking feature is that
for each point on the disk the proper xillver-reflection spectrum
is chosen for each relativistically calculated emission angle. The
implications of this improvement and more details regarding the
model are provided in Garcia & Dauser et al. (2014, ApJ, 782, 76)
and Dauser & Garcia et al. (2014, MNRAS, 444, L100). More recently returning
radiation has also been added (Dauser et al, 2022, MNRAS , 514, 3965).
relxill on GitHub:
you can also follow the development of the model on GitHub and download the model from there
(https://github.com/thdauser/relxill/)
returning radiation included (Dauser et al, 2022, MNRAS , 514, 3965,
link
)boost parameter instead of the reflection
fractionrelxilllpCp model with ionization and density gradient (up to 1020cm-3)
and a velocity of the lamp post sourcerelxill model,
including a detailed explanation of all features
(relxill_docu_v1.0.pdf)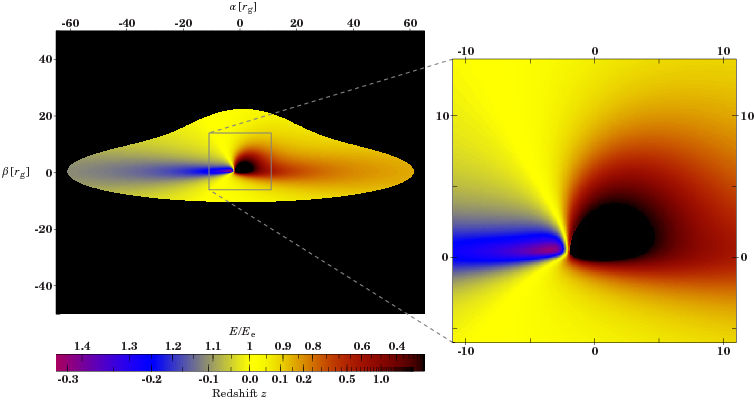
relxill model
package
xillver reflection model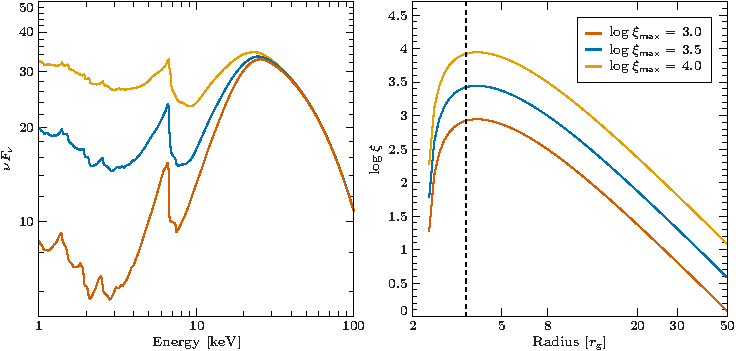
relxill model
As of version 1.3.0, the relxill also includes a variant which
allows for an ionization gradient. Currently this is implemented for the relxilllpCp model flavor.
Either the shape of the gradient can be
fitted as a power law, or the gradient is predicted from the alpha disk
density profile.
The figure on the left shows the spectra for three different levels of ionization (left panel) with the associated ionization gradient (right panel). The dashed line shows the radius of maximal ionization.
First download all necessary files given in the download section. It is not necessary to download all reflection tables. If those are required, a warning is issued when executing the model.
To compile the model, put all the downloaded files into a directory, and unpack them:
tar xfz relxill_tables.tgz tar xfz relxill_model_v2.3.tgz
In order to compile the model, it is recommended that you call the provided compile-script by executing:
chmod u+x ./compile_relxill.sh ./compile_relxill.sh
In this way the path to the tables will be correctly set in the model code, allowing you to properly load the model from any location. If you have a Mac OSX and setting the table paths fails, you might need to edit the file and un-comment the line marked for "Mac OSX".
ALTERNATIVE: If you don't want to use this compile script, you can also set the path to the tables by setting the environment variable "RELXILL_TABLE_PATH" to the directory which contains the tables.
For Mac Users (taken from the Xspec webpage for Xspec 12.13.1) [if you attempt] to build the relxill local model package with the clang++ compiler, you will first need to download and run this shell script from your heasoft-[ver]/Xspec/src directory. Note that this is the same directory from which you would normally install Xspec patch files.
relxilllpionCp added, which provides
the ionization gradient and a moving primary source, but now also for
the nthcomp primary continuum.
- 2019-08-09
relxilllpion model
- 2019-08-02
relxilllpion
predicting an ionization gradient (more information is given
in the model section) xillverD, relxillD) to include a larger
range in Gamma up to 3.6 (table is now xillverD-5.fits)
- 2019-07-12relxilllp and relxilllpCp,
affecting only LP sources at large height (>20Rg) and
Rout<1000 Rg, or with Rin>R_ISCO. The spectral shape and
therefore eventually fitting parameters were only affected
if fixReflFrac=1,2 was set. Additionally, problems
with caching which sometimes occured when changing the
inclination by a large were also fixed. - 2018-03-07relxilllpCp
temperature is now correctly given in the rest frame of the
primary source - 2017-12-06relxill
model, including now multiple zones for the LP-relxill
model flavours. All other models produce the same results,
but all models are evaluated significantly faster - 2017-06-08relxill model flavors The detailed documentation can be found in the Download Section. In the following only a brief overview of the models is given.

Standard relativistic reflection model, modeling the irradiation of the accretion by a broken power law emissivity. Different flavors are for an incident spectrum by either the standard high-energy cutoff powerlaw or an nthcomp Comptonization continuum (Cp).

The relativistic reflection model for the lamp post geometry, again for an incident cutoff powerlaw or nthcomp spectrum (Cp). The disk is split in multiple zones, which see a different incident spectrum due to relativistic energy shifts of the primary spectrum.

normal reflection models, given for different incident spectra; powerlaw with high-energy cutoff (xillver) or with a nthcomp Comptonization (xillverCp).

simple line model, available in the coronal and lamp post (lp) geometry

similar to the line models, but now as a convolution model being able to convolve any reflection

Model including an ionization gradient. Depending on the setting of the parameter iongrad_type, the gradient can be either modeled empirically as power law, or is predicted assuming a simple alpha disk (Shakura & Sunyaev, 1973). Detailed information is given in the parameters section. Also includes a velocity of the primary source.

Same as the standard reflection models (xillver, relxill) but with a black body of temperature kTbb as incident spectrum.
relxill model parametersIn the following, a list of all model parameters ia given. Some parameters have a special meaning if their value is negative, as also indicated in the list below. A detailed explanation of the parameters can be found in the PDF documentation.
spin of the black hole in dimensionless units, negative values mean the accretion disk is counter-rotating with respect to the black hole
inner and outer radius of the accretion disk in gravitational radii. Can also be given in units of the ISCO, when it is set to negative values.
inclination towards the system with respect to the normal to the accretion disk
the emissivity for the coronal flavor models is given as r-Index1 between Rin and Rbr and r-Index2 between Rbr and Rout. Rbr is measured in gravitational radii, but can also be given in units of the ISCO if given in negative values.
Height of the primary source above the black hole in gravitational radii. Can be given in units of the event horizon if set to negative values.
Velocity of the primary source, in units v/c. Allowed values range form 0 to 0.99.
reflection fraction, defined in the frame of the primary source as ratio of intensity emitted towards the disk compared to escaping to infinity (see Dauser+2016 for more details). If set to a negative value, only the reflected component is returned. If setting switch_reflfrac_boost=1, it is interpreted as the boost parameter, which divides the reflection fraction by the predicted value of the given lamp post geometry.
if set to 1, returning radiation is included in the model (see Dauser+22)
Ionization of the accretion disk, ranging from 0 (neutral) to 4.7 (heavily ionized). In case of an ionization gradient, it specifies either the ionization at the inner edge (power law type) or the maximal ionization at (11/9)²Rin (alpha type).
The iron abundance of the material in the accretion disk (in units of solar abundance).
Power law index of the incident spectrum.
Temperature of the black body of the incident spectrum in case of the relxillNS model.
Parameter describing the observed high energy cutoff Ecut of the primary spectrum. In case of the nthcomp input spectrum it is given as electron temperature in the corona (kTe). Important: This means that for all LP-type models, Ecut is given in the frame of the observer and therefore the value at the primary source has to be calculated by multiplying with the redshift factor (see fixReflFrac=2). kTe is given at the primary source, as temperature of the plasma. In case of the standard coronal model, no energy shift is applied.
The density of the accretion disk (in cm-3) given in logarithmic units. Models not containing this parameter are calculated for a fixed density of 1015 cm-3.
redshift to the source
Specifies the ionization gradient. If set to 1, it will be modeled as power law where the iongrad_index is defined as xi = r-iongrad_index. Setting it to 2 means it a density gradient for of an alpha disk is used, and the ionization gradient is self-consistently calculated from the irradiation of the primary source. In this case the ionization parameter is given at the maximal value (at (11/9)²Rin, see logxi above). For convenience, setting it to 0 means constant ionization.