3D orbit plots (xfig example)
Jump to navigation
Jump to search
The projection and handling of plotting in 3D is very similar to the examples Plotting in 3D (simple) and Plotting in 3D.
%-*- mode: fold; mode: slang -*-
require("isisscripts");
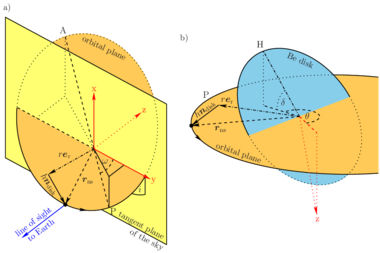
% we will produce two plots: one showing the orbital plane in the
% context of the tangent plane of the sky and, thus, defining the
% orbital elements. the second one defines the Be disk geometry
% with respect to the orbital plane only, i.e, *without* the
% tangent plane of the sky and the orbital elements.
% in the coordinate system used here, the tangent plane of the sky
% is defined as the xy-plane and the z-axis points away from Earth.
% that is with a camera inclination and roll angle of zero, we are
% looking directly onto the tangent plane of the sky. note that the
% x and y axis points north and east, respectively, i.e., the xy
% axis are flipped to ensure a right handed coordinate system.
xfig_add_latex_package("bm"); % for bold and italic fonts in mathmode
xfig_set_latex_preamble("\let\mathbfit\bm"R); % alias for MNRAS
xfig_set_font_style(NULL); % no bold face anywhere
%%% implement camera object %{{{
% set up the camera view port
private define _xfig_camera_setup(s, incl, zrot, roll) {
s.camera_data.incl = incl;
s.camera_data.zrot = zrot;
s.camera_data.roll = roll;
% update camera vectors
s.camera_data.cx = vector_rotate(
vector(1,0,0), vector(0,1,0), -s.camera_data.zrot*PI/180
);
s.camera_data.cy = vector_rotate(
vector_rotate(vector(0,1,0), vector(1,0,0), s.camera_data.incl*PI/180),
vector(0,1,0), -s.camera_data.zrot*PI/180
);
% optical axis of the camera
variable camaxis = crossprod(s.camera_data.cx, s.camera_data.cy);
% rotate around this vector
s.camera_data.cx = vector_rotate(s.camera_data.cx, camaxis, s.camera_data.roll*PI/180);
s.camera_data.cy = vector_rotate(s.camera_data.cy, camaxis, s.camera_data.roll*PI/180);
}
% add polygons to the plot
private define _xfig_camera_plot_polygon(s, v) {
% add starting point [0,0,0]
if (length(v.x) == 1 && not qualifier_exists("skiporigin")) {
v = struct_copy(v);
v.x = [0, v.x];
v.y = [0, v.y];
v.z = [0, v.z];
}
% add to list
list_append(s.camera_data.polygons, v);
list_append(s.camera_data.polygons_qualifiers, __qualifiers);
}
% add shaded region to the plot
private define _xfig_camera_shade_region(s, v) {
% add to the same list as for polygons, but set a qualifier
list_append(s.camera_data.polygons, v);
list_append(s.camera_data.polygons_qualifiers, struct_combine(
__qualifiers, struct { _camera_shade_region }
));
}
% add label to the plot
private define _xfig_camera_xyzlabel() {
variable s, v, l, dx = 0, dy = 0;
switch (_NARGS)
{ case 3: (s, v, l) = (); }
{ case 5: (s, v, l, dx, dy) = (); }
list_append(s.camera_data.labels, v);
list_append(s.camera_data.labels, l);
list_append(s.camera_data.labels, [dx, dy]);
list_append(s.camera_data.labels_qualifiers, __qualifiers);
}
% render polygons
private define _xfig_camera_render_polygons(s, pl) {
% loop over polygons
variable i;
_for i (0, length(s.camera_data.polygons)-1, 1) {
% shade region
if (s.camera_data.polygons_qualifiers[i] != NULL &&
struct_field_exists(s.camera_data.polygons_qualifiers[i], "_camera_shade_region")) {
pl.shade_region(
dotprod(s.camera_data.polygons[i], s.camera_data.cx),
dotprod(s.camera_data.polygons[i], s.camera_data.cy);;
s.camera_data.polygons_qualifiers[i]
);
}
% plot line
else {
pl.plot(
dotprod(s.camera_data.polygons[i], s.camera_data.cx),
dotprod(s.camera_data.polygons[i], s.camera_data.cy);;
s.camera_data.polygons_qualifiers[i]
);
}
}
% loop over labels
_for i (0, length(s.camera_data.labels)/3-1, 1) {
pl.xylabel(
dotprod(s.camera_data.labels[3*i], s.camera_data.cx),
dotprod(s.camera_data.labels[3*i], s.camera_data.cy),
s.camera_data.labels[3*i+1], __push_array(s.camera_data.labels[3*i+2]);;
s.camera_data.labels_qualifiers[i]
);
}
}
% new render function
private define _xfig_camera_render(s, file) {
% first render all polygons
s.camera_render_polygons(s, s);
% default xfig render
(@(s.camera_data.camera_xfig_render))(file);
}
% return an xfig_plot_new with a camera object included
define xfig_new_camera_plot() {
variable args = __pop_args(_NARGS);
variable s = struct_combine(
struct {
camera_setup = &_xfig_camera_setup,
camera_plot_polygon = &_xfig_camera_plot_polygon,
camera_xyzlabel = &_xfig_camera_xyzlabel,
camera_shade_region = &_xfig_camera_shade_region,
camera_render_polygons = &_xfig_camera_render_polygons,
camera_data = struct { % camera data
polygons = list_new, % list of polygons (Vector_Type[]) to plot
polygons_qualifiers = list_new, % plot qualifiers for each polygon
labels = list_new, % list of labels (Vector_Type[], String_Type)
labels_qualifiers = list_new, % qualifiers for each label
incl, zrot, roll, % camera inclination (around x), rotation (around z), and roll (around the optical axis)
cx, cy, % unit vectors
camera_xfig_render % remember xfig renderer function
}
},
xfig_plot_new(__push_args(args))
);
% default camera setup
s.camera_setup(0, 0, 0);
% remember xfig renderer function and then overwrite
s.camera_data.camera_xfig_render = s.render;
s.render = &_xfig_camera_render;
return s;
}
%}}}
%%% useful functions %{{{
% function to split a closed line given as an array of vectors using indices.
% ensure that the returned arrays of vectors define a line without breaks
define vecsplitsort(r, n) {
variable len = vector_norm(vector(diff(r.x[n]), diff(r.y[n]), diff(r.z[n])));
variable i = @n;
if (max(len) > 2*median(len)) {
i = shift(n, where_max(len)+1);
}
return vector(r.x[i], r.y[i], r.z[i]);
}
% function to shift, incline, and rotate a vector into the orbital plane
variable a, incl, omega, nOrb, ecc;
define vec2orbit(x) {
% translate according to the focal point (center of mass)
ifnot (qualifier_exists("notrans")) {
x += vector(-sqrt(a^2 - (a*(1-ecc))^2), 0, 0);
}
% incline
ifnot (qualifier_exists("noincl")) {
x = vector_rotate(x, vector(1, 0, 0), incl * PI/180);
}
% rotate
ifnot (qualifier_exists("noomega")) {
x = vector_rotate(
x, nOrb, omega * PI/180
);
}
return x;
}
% calculates an arch between the vectors v1 and v2 with radius r
define arch(v1, v2, r) {
v1 *= (1./vector_norm(v1));
v2 *= (1./vector_norm(v2));
% angle between the vectors and rotation axis, i.e, the normal
variable angle = acos(dotprod(v1, v2));
variable axis = crossprod(v1, v2);
axis *= (1./vector_norm(axis));
if (qualifier_exists("reverse")) {
axis *= -1;
angle = 2*PI - angle;
}
% calculate arch by rotating v1 around the axis
variable nphi = int(1000*angle/2/PI);
variable step = angle / nphi;
variable arch = Vector_Type[nphi];
variable i;
_for i (0, nphi-1, 1) {
arch[i] = r*vector_rotate(v1, axis, step*i);
}
return merge_struct_arrays(arch);
}
%}}}
%%% define geometry %{{{
% orbit parameters
variable ecc = .05, a = 300; % = 1 - b/a
variable omega = -50, incl = 30.;
% Be disk parameters
variable inclDisk = -50;
variable omegaDisk = 180+28;
variable radDisk = 150;
% neutron star's orbital plase
variable phiNS = .9;
% define normal vectors of the reference frame (plotted later)
% (note that x and y are flipped, see abow)
variable ex = vector(0,1,0);
variable ey = vector(1,0,0);
variable ez = vector(0,0,1);
%}}}
variable n, m;
%%% calculation of orbit, disk, and neutron star position and disk %{{{
% calculate orbit
variable nOrb = vector_rotate(vector(0, 0, 1), vector(1, 0, 0), incl * PI/180);
variable phi = [0:2*PI:#1000];
variable rOrb = vector(
Double_Type[length(phi)], Double_Type[length(phi)], Double_Type[length(phi)]
);
(rOrb.x, rOrb.y) = ellipse(a, a*(1-ecc), 0, phi);
rOrb = vec2orbit(rOrb);
% calculate Be disk
variable rDisk = vector(
Double_Type[length(phi)], Double_Type[length(phi)], Double_Type[length(phi)]
);
(rDisk.x, rDisk.y) = ellipse(radDisk, radDisk, 0, phi);
rDisk = vector_rotate(rDisk, vector(1, 0, 0), (incl+inclDisk) * PI/180);
rDisk = vector_rotate(rDisk, nOrb, omegaDisk * PI/180);
% disk normal
variable nDisk = vector_rotate(vector(0, 0, 1), vector(1, 0, 0), (incl+inclDisk) * PI/180);
nDisk = vector_rotate(nDisk, nOrb, omegaDisk * PI/180);
% neutron star position
variable n = wherefirstmin(abs(phi-phiNS*2*PI)); % orbital phase
variable rNS = vector(rOrb.x[n], rOrb.y[n], rOrb.z[n]);
%}}}
variable H = 12; % plot heights (width set individually)
%%% first xfig plot %{{{
variable pl1 = xfig_new_camera_plot(8.,H);
pl1.camera_setup(40, 40, 0);
variable xmin = -315, ymin = -350, wlen = 850;
variable WH = 1.*pl1.plot_data.plot_height/pl1.plot_data.plot_width;
pl1.world(xmin, xmin+wlen/WH, ymin, ymin+wlen);
pl1.axes(; major = 0, minor = 0, color = "white");
pl1.xylabel(.01, .99, "a)", -.5, .5; size = "small", world0);
% define colors
variable orbColor = "#ffca57";
variable tgColor = "#ffff71";
% xyz-axes
variable xyzlen = 250.; % arrow length
pl1.camera_plot_polygon(xyzlen*ex; forward_arrow, color = "red", depth = 20);
pl1.camera_plot_polygon(xyzlen*ey; forward_arrow, color = "red", depth = 20);
pl1.camera_plot_polygon(xyzlen*ez; forward_arrow, color = "red", line = 2);
pl1.camera_xyzlabel(1.05*xyzlen*ex, "x"; color = "red");
pl1.camera_xyzlabel(1.05*xyzlen*ey, "y"; color = "red");
pl1.camera_xyzlabel(1.05*xyzlen*ez, "z"; color = "red");
% plot orbit
n = where(rOrb.y < 0, &m);
pl1.camera_plot_polygon(vecsplitsort(rOrb, n); depth = 85);
pl1.camera_plot_polygon(vecsplitsort(rOrb, m); line = 2, depth = 85);
pl1.camera_shade_region(vecsplitsort(rOrb, n); color = orbColor, depth = 85);
pl1.camera_shade_region(vecsplitsort(rOrb, m); color = orbColor, depth = 95);
n = struct_filter(rOrb, int(length(rOrb.x)*.38); copy);
pl1.camera_xyzlabel(n, "orbital plane"R, .3, .2; size = "small", rotate = -25);
% plot tangent plane of the sky
variable tg = vector(
-390*[1,0,0,1,1] + 320*[0,1,1,0,0],
-250*[1,1,0,0,1] + 370*[0,0,1,1,0],
[0,0,0,0,0]
);
pl1.camera_plot_polygon(tg; depth = 90);
pl1.camera_shade_region(tg; color = tgColor, depth = 90);
n = -28;
pl1.camera_xyzlabel(struct_filter(tg, 1; copy), "tangent plane"R, .55, -.7; size = "small", rotate = n);
pl1.camera_xyzlabel(struct_filter(tg, 1; copy), "of the sky"R, .6, -.2; size = "small", rotate = n);
% intersection of the planes
n = wherefirstmin(abs(rOrb.y + rOrb.z));
pl1.camera_plot_polygon(vector(rOrb.x[n], 0, 0); line = 1);
% inclination angle
% find intersection of the orbit with the x-axis
n = where_min(abs(abs(rOrb.y) + rOrb.z)) + [-1,0,1];
m = interpol_points(0, rOrb.y[n], rOrb.x[n]);
pl1.camera_plot_polygon(vector([m,m], [0,-80], [0,0]); depth = 50);
pl1.camera_xyzlabel(vector(m, -60, 0), "$i$", .75, -.1);
% find the point on the orbit, which at a certain distance from this intersection point
n = where(rOrb.y < 0 and rOrb.x > 0);
n = n[where_min(abs(vector_norm(struct_filter(rOrb, n; copy) - vector(m, 0, 0)) - 80))];
% connect the intersection point and the orbit with an arch of the same length as the distance
pl1.camera_plot_polygon(vector(m, 0, 0) + arch(
vector(0, -1, 0), vector(rOrb.x[n] - m, rOrb.y[n], rOrb.z[n]), 80
));
% periastron and apastron position
variable pstrn = vec2orbit(vector(a, 0, 0));
variable astrn = vec2orbit(vector(-a, 0, 0));
pl1.camera_plot_polygon(merge_struct_arrays([pstrn, astrn]); line = 1, depth = 50);
pl1.camera_xyzlabel(pstrn, "P", -.5, .5);
pl1.camera_xyzlabel(astrn, "A", .3, -.8);
% prism supporting the 3D position of the periastron
pl1.camera_plot_polygon(merge_struct_arrays([pstrn, pstrn-vector(0,pstrn.y,0)]));
pl1.camera_plot_polygon(merge_struct_arrays([vector(pstrn.x,0,pstrn.z), vector(pstrn.x,0,0)]));
pl1.camera_plot_polygon(vector(pstrn.x, 0, pstrn.z));
% same for the apastron
pl1.camera_plot_polygon(merge_struct_arrays([astrn, astrn-vector(0,astrn.y,0)]); line = 2);
pl1.camera_plot_polygon(merge_struct_arrays([vector(astrn.x,0,astrn.z), vector(astrn.x,0,0)]); line = 2);
pl1.camera_plot_polygon(vector(astrn.x, 0, astrn.z); line = 2);
% omega angle
n = arch(vector(1, 0, 0), pstrn, 85);
m = length(n.x)/2; % vector to half of the arch (-> label)
pl1.camera_plot_polygon(n; line = 1);
pl1.camera_xyzlabel(.8*vector(n.x[m], n.y[m], n.z[m]), "$\omega$"R, 0, -.4);
% neutrons star position
pl1.camera_plot_polygon(rNS; forward_arrow, line = 1);
pl1.camera_xyzlabel(.5*rNS, "$\mathbfit{r}_\mathrm{ns}$"R, -.6, .5);
n = wherefirstmin(vector_norm(rOrb - rNS));
pl1.camera_plot_polygon(struct_filter(rOrb, n + int(.05*length(rOrb.x)) + [0,1]; copy); forward_arrow);
% neutron star position projected into the Be disk reference frame
pl1.camera_plot_polygon(rNS; sym = "circle", fill, size = .5, skiporigin);
variable rNSdiskZ = nDisk * dotprod(rNS, nDisk);
pl1.camera_plot_polygon(rNS-rNSdiskZ; forward_arrow, line = 3);
pl1.camera_plot_polygon(merge_struct_arrays([rNS-rNSdiskZ, rNS]); forward_arrow);
pl1.camera_xyzlabel(rNS-.5*rNSdiskZ, "$h\mathbfit{n}_\mathrm{disk}$"R, .6, -.2; rotate = -55);
pl1.camera_xyzlabel(.5*(rNS-rNSdiskZ), "$r\mathbfit{e}_\mathrm{r}$"R, .5, -.8);
% line of sight
pl1.camera_plot_polygon(rNS - vector([0,0], [0,0], [0,230]); color = "blue", forward_arrow);
pl1.camera_xyzlabel(rNS, "line of sight"R, .85, .6; color = "blue", size = "\small", rotate = 37);
pl1.camera_xyzlabel(rNS, "to Earth"R, .85, 1.2; color = "blue", size = "\small", rotate = 37);
%}}}
%%% second xfig plot %{{{
variable pl2 = xfig_new_camera_plot(10,H);
variable incCam = 20; % camera inclination with respect to the orbital plane
pl2.camera_setup(incl-90+incCam, 0, 0); % incl-90 -> edge on
% rotate the camera around the orbital normal
variable rotCam = 160;
pl2.camera_data.cx = vector_rotate(pl2.camera_data.cx, nOrb, rotCam*PI/180);
pl2.camera_data.cy = vector_rotate(pl2.camera_data.cy, nOrb, rotCam*PI/180);
variable xmin = -260, ymin = -270, wlen = 500;
variable WH = 1.*pl2.plot_data.plot_height/pl2.plot_data.plot_width;
pl2.world(xmin, xmin+wlen/WH, ymin, ymin+wlen);
pl2.axes(; major = 0, minor = 0, color = "white");
pl2.xylabel(.05, .87, "b)", -.5, .5; size = "small", world0);
xyzlen = 200;
pl2.camera_plot_polygon(xyzlen*ez; forward_arrow, color = "red", line = 2);
pl2.camera_xyzlabel(1.05*xyzlen*ez, "z"; color = "red");
% define colors
variable diskColor = "skyblue";
% z-axis projected onto the orbital plane
variable zdisk = xyzlen*(ez - (ez*nOrb)*nOrb);
%zdisk *= (1./vector_norm(zdisk));
pl2.camera_plot_polygon(zdisk; color = "red", line = 1);
pl2.camera_plot_polygon(merge_struct_arrays([xyzlen*ez, zdisk]); line = 2, color = "red");
% plot orbit
pl2.camera_plot_polygon(rOrb; depth = 75);
pl2.camera_shade_region(rOrb; color = orbColor, depth = 100);
n = where(.837 < phi/2/PI < .95); % nasty hack for the dotted line behin the Be disk
pl2.camera_plot_polygon(struct_filter(rOrb, n; copy); depth = 65, line = 2);
n = struct_filter(rOrb, int(length(rOrb.x)*.21); copy);
pl2.camera_xyzlabel(n, "orbital plane"R, 0, -.3; size = "small", rotate = -19);
pl2.camera_xyzlabel(pstrn, "P", .5, -.5);
% plot Be disk
n = where(dotprod(rDisk, nOrb) < 0, &m);
pl2.camera_plot_polygon(vecsplitsort(rDisk, n); depth = 70);
pl2.camera_plot_polygon(vecsplitsort(rDisk, m); line = 2, depth = 85);
pl2.camera_shade_region(vecsplitsort(rDisk, n); color = diskColor, depth = 70);
pl2.camera_shade_region(vecsplitsort(rDisk, m); color = diskColor, depth = 105);
n = struct_filter(rDisk, int(length(rDisk.x)*.15); copy);
pl2.camera_xyzlabel(n, "Be disk"R, 0, .5; size = "small", rotate = -23);
% highest point of the disk above the orbit
variable hline = vector_rotate(vector(0, 1, 0), vector(1, 0, 0), (incl+inclDisk)*PI/180);
hline = radDisk*vector_rotate(hline, nOrb, omegaDisk*PI/180);
pl2.camera_plot_polygon(hline; line = 3);
pl2.camera_xyzlabel(hline*1.1, "H");
pl2.camera_plot_polygon(hline - (hline*nOrb)*nOrb; line = 1);
pl2.camera_plot_polygon(merge_struct_arrays([hline, hline - (hline*nOrb)*nOrb]); line = 2);
% omega disk
n = arch(zdisk, hline - (hline*nOrb)*nOrb, 40; reverse);
pl2.camera_plot_polygon(n; line = 1);
pl2.camera_xyzlabel(.5*struct_filter(n, length(n.x)/2-1; copy), "$\theta$"R, 0, .1);
% disk inclination
n = arch(hline, hline - (hline*nOrb)*nOrb, 60);
pl2.camera_plot_polygon(n; line = 2);
pl2.camera_xyzlabel(.7*struct_filter(n, length(n.x)/2-1; copy), "$\delta$"R, .2, -.2);
% neutrons star position (new one compared to plot 1)
phiNS = .09;
n = wherefirstmin(abs(phi-phiNS*2*PI)); % orbital phase
rNS = vector(rOrb.x[n], rOrb.y[n], rOrb.z[n]);
pl2.camera_plot_polygon(rNS; sym = "circle", fill, size = .5, skiporigin);
pl2.camera_plot_polygon(rNS; forward_arrow, line = 1);
pl2.camera_xyzlabel(.6*rNS, "$\mathbfit{r}_\mathrm{ns}$"R, 1.1, .9);
n = wherefirstmin(vector_norm(rOrb - rNS));
pl2.camera_plot_polygon(struct_filter(rOrb, n + int(.05*length(rOrb.x)) + [0,1]; copy); forward_arrow);
% neutron star position projected into the Be disk reference frame
rNSdiskZ = nDisk * dotprod(rNS, nDisk);
pl2.camera_plot_polygon(rNS-rNSdiskZ; forward_arrow, line = 3);
pl2.camera_plot_polygon(merge_struct_arrays([rNS-rNSdiskZ, rNS]); forward_arrow);
pl2.camera_xyzlabel(rNS-.5*rNSdiskZ, "$h\mathbfit{n}_\mathrm{disk}$"R, 0, -.3; rotate = 39);
pl2.camera_xyzlabel(.9*(rNS-rNSdiskZ), "$r\mathbfit{e}_\mathrm{r}$"R, 0, -.7);
%}}}
% combine and render
% (note: the camera plot renderes the lines only when .render is called.
% thus we need to call these first, which is not a convenient way...)
pl1.render("../plots/reference_frames.pdf");
pl2.render("../plots/reference_frames.pdf");
xfig_new_hbox_compound(pl1,pl2).render("../plots/reference_frames.pdf");